2015-05-05
279
Операция сложения.
Определение. Сложением двух комплексных чисел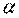 
и 
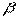называется такое комплексное число 
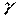с координатами 
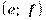, где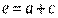 
, 
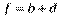, т.е. 
.
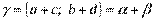Свойства:
;
;
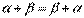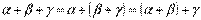
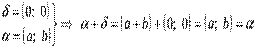для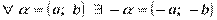
, что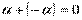 
.
Операция умножения.
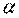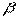Определение. Произведением двух комплексных чисел и называется такое комплексное число 
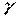с координатами 
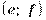, где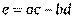 
, 
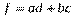, т.е. 
.
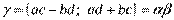Свойства:
;
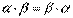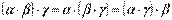
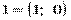, для 
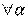
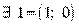, что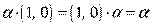 
;
для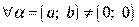
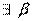, что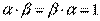 
.
Если комплексное число имеет вид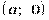 
, то данное число находится на числовой оси 
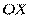и можно записать просто в виде действительного числа 
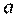, следовательно 
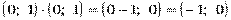. Если обозначить 
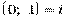, то получим, что 
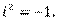Таким образом любое комплексное число 
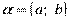можно записать в другом виде:
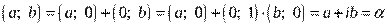, здесь 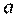и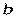 
– действительные числа, 
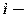мнимое число.
2) Комплексным числом z называется пара (x, y) действительных чисел x и y. При этом равенство, сумма и произведение упорядоченных пар, а также отождествление некоторых из них с действительными числами определяются следующим образом:
1) два комплексных числа z 1 = (x 1, y 1) и z 2 = (x 2, y 2) называются равными, если x 1 = x 2 и y 1 = y 2;
2) суммой комплексных чисел z 1 и z 2 называется комплексное число z вида
z = (x 1 + x 2, y 1 + y 2);
3) произведением комплексных чисел z 1 и z 2 называется комплексное число
z = (x 1 x 2 - y 1 y 2, x 1 y 2 + x 2 y 1);
4) множество комплексных чисел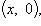 
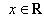, отождествляется с множеством действительных чисел R.
Разностью комплексных чисел z 1 и z 2 называется комплексное число z такое, что z 2 + z = z 1, откуда находим z = z 1 - z 2 = (x 1 - x 2, y 1 - y 2).
Частным комплексных чисел z 1 и z 2 называется комплексное число z такое, что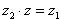 
. Отсюда находим
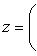
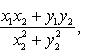
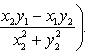
Комплексное число (0, 1) обозначается символом i = (0, 1). Тогда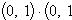 
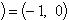, т. е. i 2 = -1. Произвольное комплексное число z можно записать в виде
z = (x, y) = (x, 0) + (0, y) = (x, 0) + (0, 1)(y, 0) = x + iy.
Эта запись называется алгебраической формой комплексного числа. Комплексное число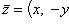 
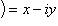называется сопряженным по отношению к комплексному числу z = (x, y) = x + iy.
Модулем комплексного числа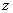 
называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длинарадиус-вектора, который на чертеже обозначен красным цветом.
Модуль комплексного числа 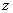стандартно обозначают: 
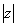или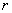 
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа: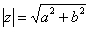 
. Данная формула справедлива для любых значений «а» и «бэ».
Аргументом комплексного числа 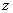называется угол 
между положительной полуосьюдействительной оси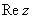 
и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: 
.
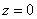Аргумент комплексного числа 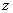стандартно обозначают: 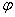или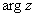 
3) Та запись комплексного числа, которую мы использовали до сих пор, называется алгебраической формой записи комплексного числа. Часто бывает удобна немного другая форма записи комплексного числа. Пусть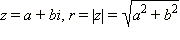 
и φ = arg z. Тогда по определению аргумента имеем:
|
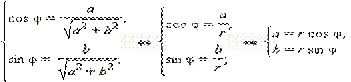
Отсюда получается
| z = a + bi = r (cos φ + i sin φ). |
Такая форма называется тригонометрической формой записи комплексного числа. Как видно, для того, чтобы перейти от алгебраической формы записи комплексного числа к тригонометрической форме, нужно найти его модуль и один из аргументов.
