Формулы Крамера

Рассмотрим систему линейных уравнений с квадратной матрицей (А_nn):

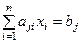(j = 1, 2, …, n). Умножим обе части этого равенства на 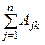. Получим справа: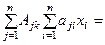 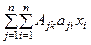= = x_k det A, и слева: .

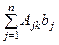Отсюда получим: .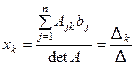

Здесь через ∆ обозначен det A, называемый главным определителем (определитель матрицы системы). Через ∆ _k обозначены определитель матрицы А_k, который получается из матрицы системы А заменой k ^го столбца на столбец свободных членов.

Доказана теорема Крамера:

Т°. Если ∆ ¹ 0, то система Ax = b имеет единственное решение, которое задается формулами

Крамера: x_k = 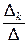, k = 1, 2, …, n.