Обратная матрица. Если для квадратной матрицы А существует матрица D, такая что DА = АD = Е, то матрица D называется матрицей обратной к матрице А и обозначается: D = A–1

Если для квадратной матрицы А существует матрица D, такая что DА = АD = Е, то матрица D называется матрицей обратной к матрице А и обозначается: D = A ^–1.

1°. Если A ^–1 существует, то она единственна.

◀ . ▶

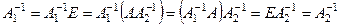2°. (A ^–1)^–1 = A. ◀ A = AE = A (A ^–1(A ^–1)^–1) = (AA ^–1) (A ^–1)^–1 = E (A ^–1)^–1 = (A ^–1)^–1. ▶

3°. (AB)^–1 = B ^–1 A ^–1.

◀ B ^–1 A ^–1 = B ^–1 A ^–1 E = B ^–1 A ^–1((AB)×(AB)^–1(AB)) = B ^–1(A ^–1 A) B ×(AB)^–1 = B ^–1 B (AB)^–1 = (AB)^–1. ▶

4°. det(A ^–1) = (det A)^–1. ◀ AA ^–1 = E Þ det AA ^–1 = det A ×det(A ^–1) = 1 Þ det(А ^–1) = 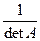. ▶ 5°. Чтобы квадратная матрица А имела обратную А ^–1 необходимо и достаточно, чтобы det A ¹ 0.

Если det A ¹ 0, то матрица А называется невырожденной.

◀ Необходимость. $ А ^–1 Þ det(A ^–1) = 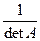Þ det A ¹ 0.

Достаточность. Возьмем матицу D с элементами

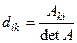Þ (DA) _ij = . ▶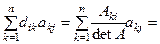

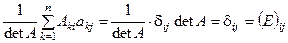Доказательство теоремы одновременно дало и способ построения матрицы, обратной к невырожденной матрице А. Чтобы построить матрицу обратную к А, надо:

найдем det A. Если det A = 0, то А ^–1 не существует. Если det A ¹ 0, то продолжаем построение обратной матрицы;

для элементов a_ij матрицы А найдем их алгебраические дополнения A_ij;

разделим матрицу из алгебраических дополнений на det A;

транспонировав полученную матрицу, получим матрицу А ^–1.

Пример: 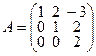: 1. det A = 2. 2. А ^–1 = .

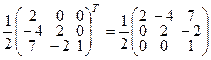В идеологии обратной матрицы решение квадратных систем с невырожденной матрицей становится весьма прозрачным: Ax = b Þ A ^–1 Ax = A^–1 b Þ x = A ^–1 b.

Есть и другие способы нахождения обратной матрицы.

А.

Запишем матрицу А, а справа от нее, через вертикальную черту, запишем единичную матрицу. Получим матрицу n – строк, 2 n – столбцов;

В получившейся матрице с помощью применения к строкам (и только) преобразований не изменяющих ранг матрицы образуем на месте матрицы А – единичную матрицу.

На месте единичной матрицы будет стоять А ^–1.

Б.

Справа от матрицы припишем единичную матрицу Е, а снизу припишем матрицу (– Е). В правом нижнем углу поставим нулевую матрицу.

Используя операции только над строками, получившейся матрицы, на месте матрицы (– Е), образуем нулевую матрицу.

Тогда, в правом нижнем углу будет стоять А ^–1.

В.

Для обращения матрицы, имеющей блочную структуру, т.е. матрицы вида: 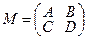, где А – квадратная матрица порядка n ´ n, а D – квадратная матрица q ´ q, справедливы следующие формулы:

Первая формула Фробениуса (если det A ¹ 0):

, где H = D – CA ^–1 B.

Вторая формула Фробениуса (если det D ¹ 0):

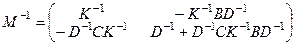, где K = A – BD ^–1 C.