Задание диграфов с помощью множеств

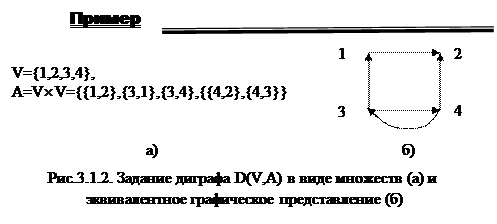
Диграфом D(V,A) является:

· конечное непустое множество V вершин;

· конечное множество А дуг, задаваемое функцией декартового произведения вершин V 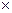V (т.е. у диграфа {v_i,v_j}≠{v_j,v_i}. Если имеется дуга е={v_i, v_j}, то говорят, что дуга направлена из вершины v_i в вершину v_j.)

Диграф D=(V,A) называется пустым, если |V|=0, |A|=0. Тривиальный диграф – это диграф D=(V,A) с |V| 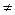0 и |A|=0.

Две вершины, соединенные дугой любого направления, являются смежными.

Говорят, что:

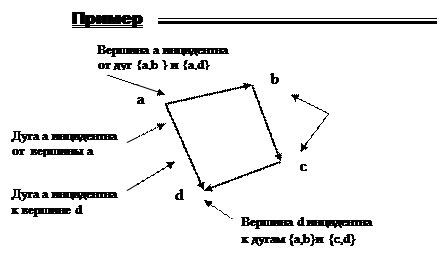
· вершина v инцидентна к дуге {v,u}, если голова дуги соединена с вершиной v;

· вершина v инцидентна от дуги {v,u}, если хвост дуги соединен с вершиной v;

· дуга {v,u} инцидентна к вершине v, если голова дуги соединена с вершиной v;

· дуга {v,u} инцидентна от вершины v, если хвост дуги соединен с вершиной v.

		Рис.3.1.3. Смежные вершины, инцидентные вершины и дуги диграфа

· |D| - порядок диграфа: число вершин диграфа D;

· ||D||- размер диграфа: число дуг диграфа.

Диграф будет конечным или бесконечным в зависимости от величины порядка диграфа |D|.

3.1.3. Полустепени диграфа

Если {u,v} – дуга диграфа, то говорят, что вершина u является входящим соседом вершины v. Симметрично, вершина v называется исходящим соседом вершины u. Множество входящих соседей вершины u обозначается Г^-_G(u)= {v V(G):{u,v} A(G)}, а множество исходящих соседей – Г⁺_G(u)= {v V(G):{u,v} A(G)}.

Полустепень исхода вершины u (обозначается deg⁺(u)) диграфа D равна |Г⁺_G(u)| (т.е. количеству дуг, инцидентных от вершины u), а полустепень захода вершины u (обозначается deg^-(u)) равна | Г^-_G(u)| (т.е. количеству дуг, инцидентных к вершине u).

Степенью вершины v диграфа D является сумма полустепеней захода и исхода вершины: deg(v) = deg⁺(v) + deg^-(v).

Истоком называется вершина s со степенью захода deg^-(s)=0, а стоком – вершина t со степенью исхода deg^-(t)=0.

Вершины	deg+(Vi)	deg-(Vi)	deg(Vi)
V1
V2
V3
V4
V5
V6
V7

· Полустепень исхода вершины deg⁺(V_i).

· Полустепень захода вершины deg^-(V_i).

· Степень вершины deg(V_i).

· Максимальная и минимальная полустепени исхода диграфа – Δ⁺(D)={max{deg⁺(V_i) | V_i V} и δ⁺(D)={min{deg⁺(V_i) | V_i V}.

· Максимальная и минимальная полустепени захода диграфа –

Δ^-(D)={max{deg^-(V_i) | V_i V} и δ^-(D)={min{deg^-(V_i) | V_i V}.

Cумма полустепеней исхода и сумма полустепеней захода вершин диграфа равна числу дуг:

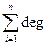⁺(v_i) = 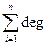^-(v_i) = m; n=│V│; m=│А│.