Метод максимального правдоподобия

Метод предложен Р. Фишером в 1912 г. Метод основан на исследовании вероятности получения выборки наблюдений (x₁, x_2, …, x_n). Эта вероятность равна

f(х₁, Θ) f(х₂, Θ) … f(х_п, Θ) dx₁ dx₂ … dx_n.

Совместная плотность вероятности

L(х₁, х₂ …, х_n; Θ) = f(х₁, Θ) f(х₂, Θ) … f(х_n, Θ), (2.7)

рассматриваемая как функция параметра Θ, называется функцией правдоподобия.

В качестве оценки Θ* параметра Θ следует взять то значение, которое обращает функцию правдоподобия в максимум. Для нахождения оценки необходимо заменить в функции правдоподобия Т на q и решить уравнение

dL/d Θ* = 0.

Для упрощения вычислений переходят от функции правдоподобия к ее логарифму ln L. Такое преобразование допустимо, так как функция правдоподобия – положительная функция, и она достигает максимума в той же точке, что и ее логарифм. Если параметр распределения векторная величина

Θ* =(q₁, q₂, …, q_n),

то оценки максимального правдоподобия находят из системы уравнений

d ln L(q₁, q₂, …, q_n) /d q₁ = 0;

d ln L(q₁, q₂, …, q_n) /d q₂ = 0;

. ........

d ln L(q₁, q₂, …, q_n) /d q_n = 0.

Для проверки того, что точка оптимума соответствует максимуму функции правдоподобия, необходимо найти вторую производную от этой функции. И если вторая производная в точке оптимума отрицательна, то найденные значения параметров максимизируют функцию.

Итак, нахождение оценок максимального правдоподобия включает следующие этапы: построение функции правдоподобия (ее натурального логарифма); дифференцирование функции по искомым параметрам и составление системы уравнений; решение системы уравнений для нахождения оценок; определение второй производной функции, проверку ее знака в точке оптимума первой производной и формирование выводов.

Пример 2.3. Будем считать, что случайная величина Х имеет нормальное распределение. Необходимо найти оценки максимального правдоподобия параметров m и S этого распределения.

Решение. Функция правдоподобия для выборки ЭД объемом n

.

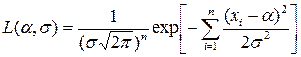
Логарифм функции правдоподобия

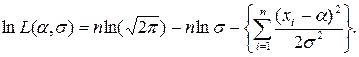
Система уравнений для нахождения оценок параметров

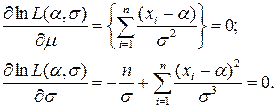
Из первого уравнения следует: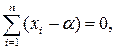

или окончательно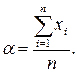

Таким образом, среднее арифметическое является оценкой максимального правдоподобия для математического ожидания.

Из второго уравнения можно найти

.

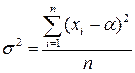Эмпирическая дисперсия является смещенной. После устранения смещения

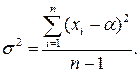
Фактические значения оценок параметров: m =27,51, s² = 0,91.

Для проверки того, что полученные оценки максимизируют значение функции правдоподобия, возьмем вторые производные

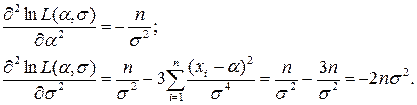
Вторые производные от функции ln(L(m,S)) независимо от значений параметров меньше нуля, следовательно, найденные значения параметров являются оценками максимального правдоподобия.

Метод максимального правдоподобия позволяет получить состоятельные, эффективные (если таковые существуют, то полученное решение даст эффективные оценки), достаточные, асимптотически нормально распределенные оценки. Этот метод может давать как смещенные, так и несмещенные оценки. Смещение удается устранить введением поправок. Метод особенно полезен при малых выборках.