Нормальное распределение. Этот вид распределения является наиболее важным в связи с центральной предельной теоремой теории вероятностей: распределение суммы независимых случайных

Этот вид распределения является наиболее важным в связи с центральной предельной теоремой теории вероятностей: распределение суммы независимых случайных величин стремится к нормальному с увеличением их количества при произвольном законе распределения отдельных слагаемых, если слагаемые обладают конечной дисперсией. Кроме того, А.М. Ляпунов доказал, что распределение параметра стремится к нормальному, если на параметр оказывает влияние большое количество факторов и ни один из них не является превалирующим. Функция плотности нормального распределения

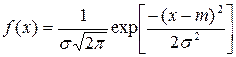(3.1)

– унимодальная, симметричная, аргумент х может принимать любые действительные значения, рис. 3.5.

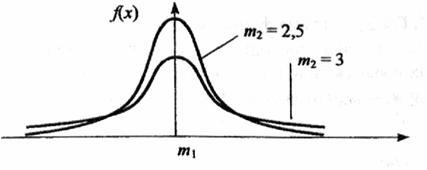
Рис. 3.5. Плотность нормального распределения

Функция плотности нормального распределения стандартизованной величины U имеет вид

.

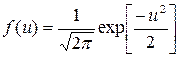Вычисление значений функции распределения Ф(u) для стандартизованного неотрицательного аргумента u (u,0) можно произвести с помощью полинома наилучшего приближения:

Ф(u) = 1– 0,5(1 + 0,196854 u + 0,115194 u² + 0,000344 u³ + 0,019527 u⁴)– 4. (3.2)

Такая аппроксимация обеспечивает абсолютную ошибку не более 0,00025. Для вычисления Ф(u) в области отрицательных значений стандартизованного аргумента u (u <0) следует воспользоваться свойством симметрии нормального распределения

Ф(u) = 1 – Ф(–u).

Иногда в справочниках вместо значений функции Ф(u) приводят значения интеграла вероятностей (для u > 0)

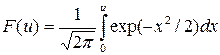(3.3)

Интеграл вероятностей связан с функцией нормального распределения стандартизованной величины u соотношением

Ф(u) = 0,5 + F(u).

3.2.2. Распределение χ² (хи-квадрат)

Распределению хи-квадрат (χ²-распределению) с k степенями свободы соответствует распределение суммы 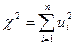квадратов n стандартизованных случайных величин u_i, каждая из которых распределена по нормальному закону, причем k из них независимы, n>k. Функция плотности χ²-распределению с k степенями свободы

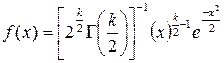, x > 0, (3.4)

где х = χ ², Г (k/2) – гамма-функция.

Число степеней свободы k определяет количество независимых слагаемых в выражении для χ ². Функция плотности при k, равном одному или двум, – монотонная, а при k >2 – унимодальная, несимметричная, рис. 3.6.

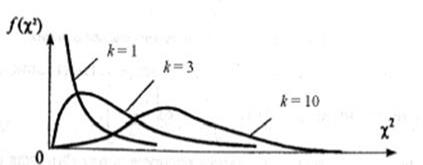
Рис. 3.6. Плотность χ²-распределение

Математическое ожидание и дисперсия величины χ² равны соответственно k и 2k. χ²-распределение является частным случаем более общего гамма-распределения, а величина, равная корню квадратному из χ² с двумя степенями свободы, подчиняется распределению Рэлея.

С увеличением числа степеней свободы (k >30) χ²-распределение приближается к нормальному распределению с математическим ожиданием k и дисперсией 2k. В таких случаях критическое значение χ ²(k;a)» u_{1– a}(k,2k), где u_1–a(k,2k) – квантиль нормального распределения. Погрешность аппроксимации не превышает нескольких процентов.