2015-05-05
720
С геометрической точки зрения интегральная сумма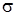 
представляет собой сумму площадей прямоугольников, основаниями которых являются частичные отрезки 
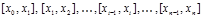, а высоты равны 
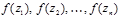соответственно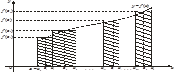 
Рис. 1
Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка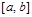 
на частичные отрезки, ни от выбора точек 
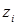в них, то этот предел называется определенным интегралом от функции 
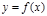на отрезке 
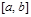и обозначается 
.
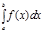Таким образом,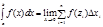 
.
В этом случае функция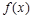 
называется интегрируемой на 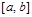. Числа а и b называются соответственно нижним и верхним пределами интегрирования, 
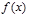– подынтегральной функцией, 
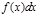– подынтегральным выражением, 
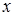– переменной интегрирования; отрезок 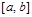называется промежутком интегрирования.
Теорема 1. Если функция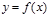 
непрерывна на отрезке 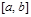, то она интегрируема на этом отрезке.
2. Геометрический смысл определенного интеграла
Пусть на отрезке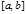 
задана непрерывная неотрицательная функция 
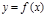. Криволинейной трапецией называется фигура, ограниченная сверху графиком функции y = f(x), снизу – осью Ох, слева и справа – прямыми x = a и x = b (рис. 2).
|
|
|
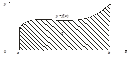
Рис. 2
Определенный интеграл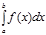 
от неотрицательной функции 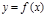с геометрической точки зрения численно равен площади криволинейной трапеции, ограниченной сверху графиком функции 
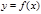, слева и справа – отрезками прямых 
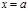и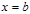 
, снизу – отрезком 
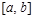оси Ох.
