Участок 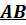 .
.
Дифференциальное уравнение движения:
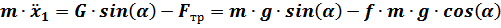
или
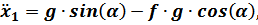
где
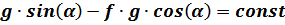 .
.
После первого интегрирования получаем:
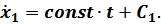
Константа 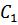 определяется из начальных условий:
определяется из начальных условий:
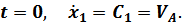
После второго интегрирования получаем:
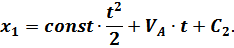
Из начальных условий:
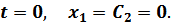
Конец участка 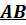 .
.
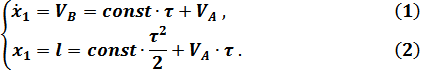
В полученной системе из двух уравнений три неизвестных 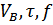 . На данном этапе эта система неразрешима. Величину
. На данном этапе эта система неразрешима. Величину 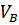 можно будет определить, рассмотрев движение на участке
можно будет определить, рассмотрев движение на участке 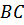 .
.
Участок 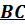 .
.
Свободное падение под действием силы гравитации 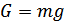 без учёта сопротивления воздуха (рис. 33):
без учёта сопротивления воздуха (рис. 33):
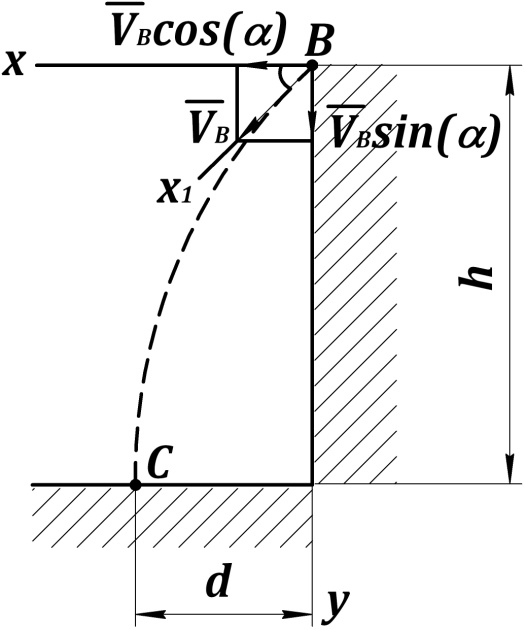
Рис. 38. Участок 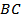
Горизонтальная скорость постоянная; горизонтальное ускорение (торможение) отсутствует.
Система дифференциальных уравнений будет иметь вид:
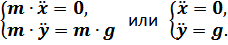
После первого интегрирования получаем:
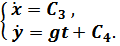
Из начальных условий:
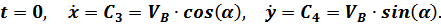
После второго интегрирования получаем:
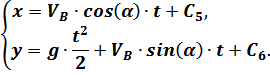
Из начальных условий:
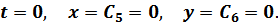
Конец участка 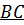 :
:
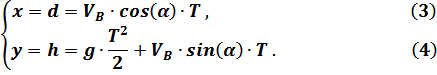
В двух уравнениях (3) и (4) два неизвестных 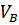 и
и 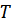 . Система разрешима.
. Система разрешима.
Из уравнения (3):
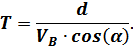
После подстановки величины 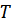 в уравнение (4) получаем уравнение с одной неизвестной величиной
в уравнение (4) получаем уравнение с одной неизвестной величиной 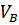 :
:
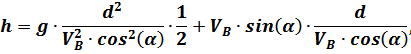
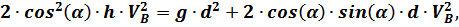
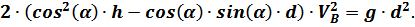
Промежуточные вычисления:
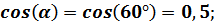
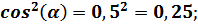
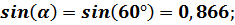
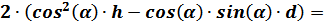
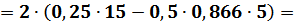
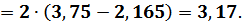
Итак, первая искомая величина будет равна:
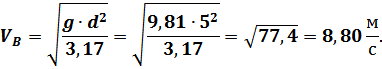
Теперь можно решать систему уравнений (1) и (2), в которой осталось два неизвестных 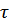 и
и 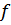 . Из уравнения (1) тогда получим:
. Из уравнения (1) тогда получим:
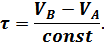
После подстановки выражения для 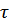 в уравнение (2) получим:
в уравнение (2) получим:
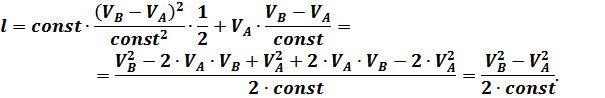
Из полученного выражения:
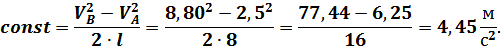
Теперь можно вычислить вторую искомую величину:
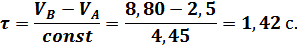
Ответ
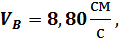
 2015-05-06
2015-05-06 363
363








