2015-05-06
382
На перемещаемое тело 1 действует проекция силы веса на плоскость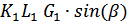 
. Она совершает положительную работу на перемещении 
:
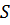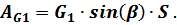
От нормальной (перпендикулярной к плоскости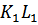 
) реакции 
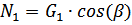возникает сила трения:
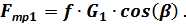
Эта сила совершает отрицательную работу на перемещении :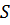
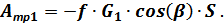
Собственно реакция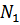 
, перпендикулярная направлению движения тела 1 по плоскости 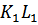, работы не совершает.
Также не совершают работу силы, возникающие в барабане 2: сила веса барабана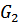 
и реакция подшипника, имеющая проекции в вертикальной плоскости 
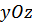, приложены к неподвижной точке 
.
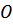Отрицательной работой является работа по подъёму катка 3 по плоскости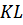 
при перемещении 
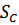центра масс катка против проекции силы его веса на эту плоскость:
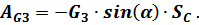
Работа силы сцепления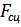 
(силы трения покоя), препятствующей скольжению катка, равна нолю, так как эта сила приложена в неподвижном мгновенном центре скоростей в точке касания катка плоскости .
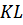При движении катка 3 необходимо преодолевать момент сопротивления качению, возникающий от нормальной (перпендикулярной к плоскости 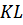) реакции 
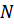от силы веса 
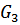; задан коэффициент трения качения 
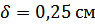. Тогда момент сопротивления равен:
|
|
|
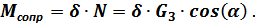
Отрицательная работа этого момента на угле поворота катка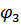 
будет:
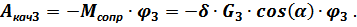
В промежуточном итоге получается:
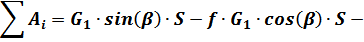
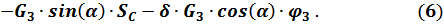
Перемещение центра масс 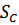катка 3 определяется через перемещение 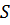тела 1 из выражения для угла поворота 
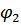барабана 2:
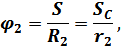
отсюда
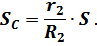
Тогда
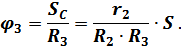
После подстановки выражений для 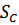и 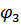в выражение (6) получается:
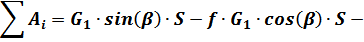
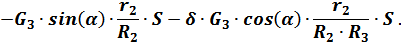
С учётом, что
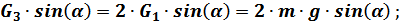
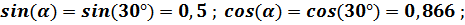
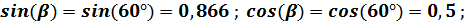
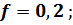
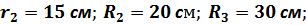
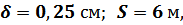
получаем расчётную формулу:
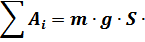
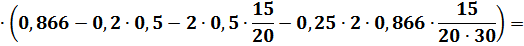
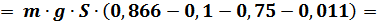
Приравняв выражения (2.5) и (2.7) для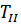 
и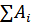 
, получаем:
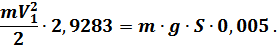
Отсюда:
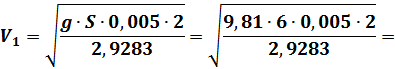
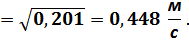
Ответ
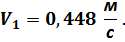
ВАРИАНТ 2
