Принципы многоканальной фильтрации

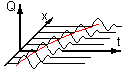
Сейсмическое волновое поле существует в трехмерном пространстве (x,y,z) и изменяется во времени (Q(x,y,z,t)), т.е. может быть изображено лишь в пятимерном пространстве.

При наблюдениях на дневной поверхности и введении статических поправок (“перенесении” ПП и ПВ на плоскость приведения) размерность уменьшается до четырех (Q(x,y,t)).

При профильных наблюдениях волновое поле изображается в трехмерном пространстве (Q(x,t)).

В частотной (спектральной) области аргументам сейсмического сигнала Q соответствуют: t ~ w; x ~ k_x = 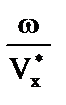; y ~ k_y = 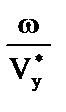; z ~ k_z = ,
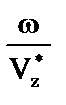где w – “временная” частота, k_x, k_y, k_z – “пространственные” частоты (волновые числа), а V_x, V_y, V_z – кажущиеся скорости волны по направлениям x, y и z, соответственно. Спектральные характеристики многомерного волнового поля могут быть получены с помощью многомерного Фурье-преобразования. Например: вдоль профиля (вдоль оси Ох) распространяется с постоянной кажущейся скоростью плоская волна

f(t,x) = f(t – (x/V^*)), где V^*= V^*_x = const(x)

(Если волна f(t,x) – гармоническая, то можно записать:

f(t,x) = 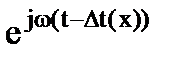= = 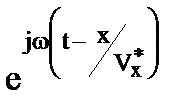= 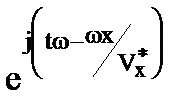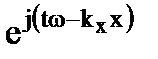где k_x = 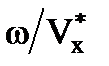= = 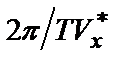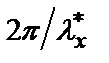(25)

Спектр f(t,x) может быть получен с помощью двумерного Фурье-преобразования:

f(t,x) Û F(w,kx) = 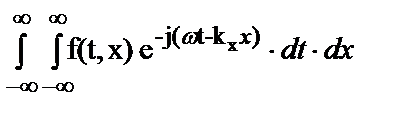F(w,kx) Û f(t,x) =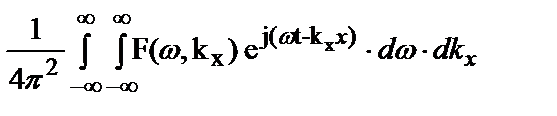

(26)

Т.О. многомерность сейсмического волнового поля (сейсмической записи) предполагает возможность фильтрации не только по t (по w), но и по x, y, z (по k_x, k_y, k_z) и по любому их сочетанию, т.е. многомерная фильтрация обладает существенно большими возможностями, чем одномерная

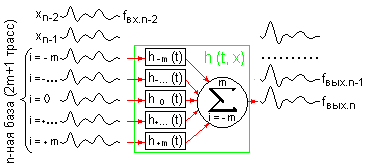
Практическая реализация многомерной фильтрации состоит в последовательном применении одномерных фильтров.

(Ниже на рисунке приведена схема двумерной многоканальной фильтрации с нечетным числом каналов на базе обработки, равным M = 2n+1, результат обработки относится к х-координате центральной трассы базы.)