Расчетные методы оценки надежности

2.1.1. Расчет надежности на основе моделей математической логики.

Расчет надежности технических средств на основе моделей математической логики осуществляется в следующей последовательности:

1. Словесная формулировка условий работоспособности средства.

Пусть дана структура тракта передачи данных, состоящего из элементов а, в, с, d, e (рис. 2.1.).

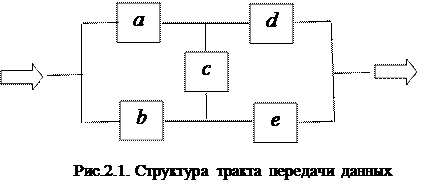Словесная формулировка минимального необходимых условий работоспособности тракта выглядит следующим образом:

«Тракт работоспособен, если работоспособны каналы (элементы): 1) а и d или 2) a и c и e или 3) b и е или 4) b и c и d».

2. Запись логической функции работоспособности .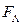

При записи логической функции работоспособности используются основные логические операции математической логики: дизъюнкция (или) -Ú ÚÙÙ***, конъюнкция (и) - *, отрицание (не) - -.

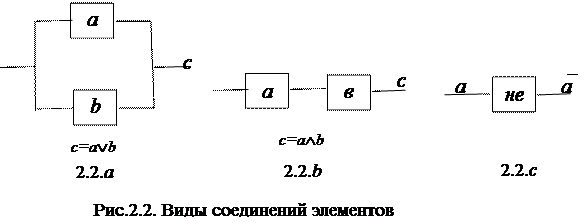
2.2. a. Параллельное соединение элементов (операция дизъюнкции) с=a Ú b.

2.2. b. Последовательное соединение (конъюнкция) с=a Ù b или с=a * b.

2.2.c.Инвертирование входной величины (операция отрицания) 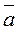- - не (a).

Таким образом, логическая функция работоспособности для рассматриваемого примера может быть представлена в виде:

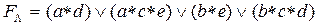
3. Преобразование 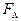путем ее минимизации и исключения повторяющихся членов.

Для этого используют следующие формулы математической логики:

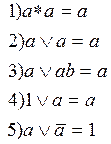
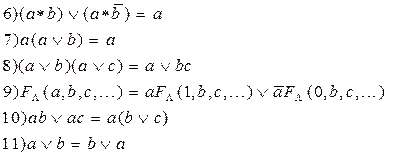
Используя формулу 9) разложим исходную 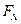с целью исключения повторяющихся членов и получим:

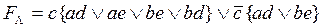
Упростим выражение в первых фигурных скобках, используя формулы (10)-дистрибутивность и 11-коммутативность)) булевой алгебры.

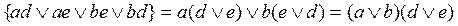
Окончательная логическая функция работоспособности принимает вид:

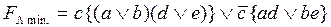
4. Замена в 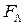логических операндов на арифметические (получение ).

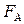Замена осуществляется по следующим правилам:

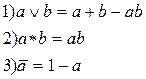
Используя правила, преобразуем 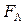в 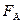, т.е. получаем функцию работоспособности в арифметическом виде:

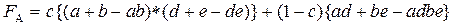
5. Замена в 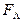простых событий их вероятностями

В выражении 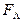простые события (высказывания) a, b, c, d, e заменяют на их вероятности P_a, P_b, P_c, P_d, P_e и получают формулы для расчета вероятности работоспособного состояния сложного технического средства:

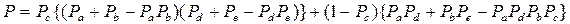
6. Подстановка в полученную формулу для P числовых значений вероятностей состояний элементов и расчет значения P.