1.2. Расчет надежности на основе моделей теории вероятностей
Рассмотрим применение моделей теории вероятностей для расчета надежности на примере определения средней наработки на отказ - T 0.
 1. Имеется резервированный объект, состоящий из двух элементов:
1. Имеется резервированный объект, состоящий из двух элементов:
Число состояний объекта - три:
1) S 0 - два элемента, входящие в объект работоспособны.
2) S 1 - один из элементов, входящих в объект, в состоянии отказа.
3) S 2 - оба элемента, входящие в объект, в состоянии отказа.
2. Граф состояний объекта имеет вид:
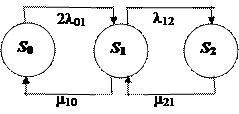 |
где 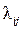 - постоянная интенсивность перехода из состояния i в состояние j;
- постоянная интенсивность перехода из состояния i в состояние j;
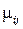 - постоянная интенсивность перехода из i в j (восстановление).
- постоянная интенсивность перехода из i в j (восстановление).
3. Вероятность каждого состояния определяется системой дифференциальных уравнений. Получить такую систему можно непосредственно по виду графа состояний по следующим правилам:
а) Для каждого из возможных состояний объекта записывается уравнение, в левой части которого 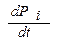 , а справа - столько слагаемых, сколько стрелок графа соприкасается с данным состоянием.
, а справа - столько слагаемых, сколько стрелок графа соприкасается с данным состоянием.
б) Если стрелка направлена в данное состояние, то перед слагаемым ставится +, если из данного состояния, то ставится знак -.
с) Каждое из слагаемых будет равно произведение интенсивности перехода из данного состояния (либо в данное состояние) на вероятность состояния, из которого выходит стрелка.
Используя эти правила получим систему дифференциальных уравнений:
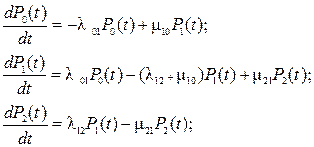
Исключая из полученной системы все неработоспособные состояния (в данном случае 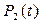 ) получим:
) получим:
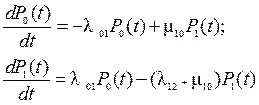
4. К последней системе уравнений применим преобразование Лапласа:
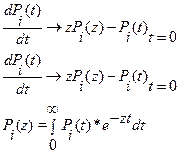
В результате получаем систему уравнений (*):
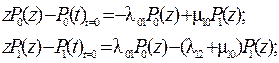
В начале работы система полностью работоспособна (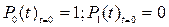 ). Тогда:
). Тогда:
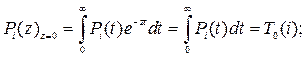
Система (*) приобретает следующий вид:
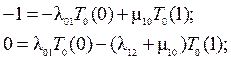
5. Решая полученную систему уравнений, находим:
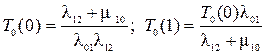
Если принять 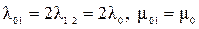 , то
, то 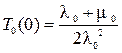 , то средняя наработка объекта на отказ будет иметь следующий вид:
, то средняя наработка объекта на отказ будет иметь следующий вид:
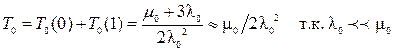 .
.
 2015-05-06
2015-05-06 621
621








