Скалярное произведение любой кодовой комбинации на проверочный вектор равно нулю

Обозначим проверочный вектор через 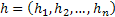; а кодовую комбинацию через 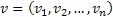, тогда их скалярное произведение равно .

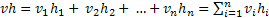Сумма берется по всем слагаемым, в которых 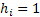, т.е. сводится к сумме элементов кодовой комбинации, охваченных проверкой на четность, а поэтому эта сумма должна быть равна 0.

Записывая проверочные векторы в прямоугольную таблицу, получим проверочную матрицу кода, обозначаемую H(n,k) и имеющую размерность (n-k)*k.

Единицы на позициях, соответствующих информационным элементам в кодовой комбинации, указывают на то, какие информационные элементы участвуют в формировании проверочного элемента, а единица на позициях избыточных элементов, указывает какой именно проверочный элемент образован данной суммой информационных элементов.

Для порождающей и проверочной матрицы справедливо равенство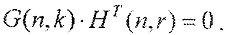

Решение данного матричного уравнения позволяет установить вид проверочной матрицы.

Проверочная матрица формируется следующим образом – в начале строится единичная матрица 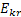после чего к ней приписывается матрица 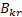содержащая k столбцов и r строк, причем каждая ее строка соответствует столбцу проверочной подматрицы 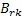порождающей матрицы, т.е.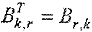

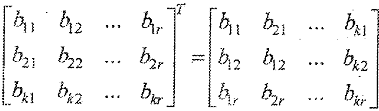
В результате проверочная матрица имеет вид

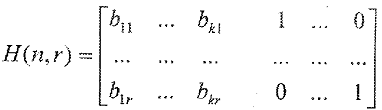
Или 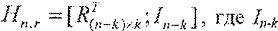- единичная матрица размерности .

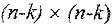Введение проверочной матрицы позволяет нормализовать процесс вычисления проверочных соотношений для любой кодовой комбинации, сведя ее к произведению кодовой комбинации на проверочную матрицу по следующему правилу: 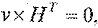(4.6) т.е. некоторая комбинация v принадлежит (n, k) – коду 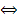она ортогональна каждой стороне матрицы H(n,k).

Соотношение (4.6) лежит в основе процедуры декодирования для линейных блочных кодов.

В результате умножения принятой комбинации на проверочную матрицу получаем вектор из (n-k) символов, называемый синдромом.

В случае если синдром нулевой, то кодовая комбинация считается принятой без ошибочно в противном случае фиксируется наличие ошибок в кодовой комбинации.

Для любого ЛБК задача декодирования может быть решена следующим образом:

Предварительно определяются виды синдромов для возможных вариантов искажений кодовых комбинаций.

В декодере производится расчет синдрома.

Производится определение позиции ошибки, соответствующей рассчитанному синдрому.

Производится коррекция кодовой комбинации.