1). y= - 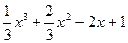 ;
;
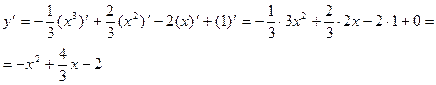
2). 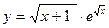 ;
;
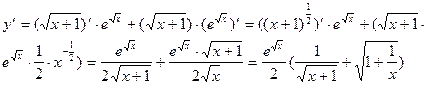
3). 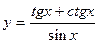 ;
;
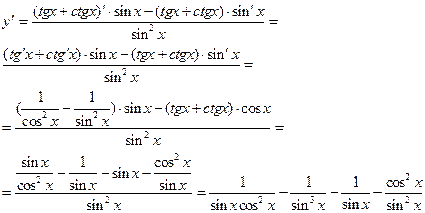
Задания для самостоятельного решения и решения у доски.
Найти производные следующих функций:
1. y=x3+2x2+8;  =
=
2. y=2 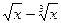 ;
;  =
=
3. y=xa+b;  =
=
4. y=(1-4x3)(1+2x2);  =
=
5. y=2x- 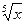 ;
;  =
=
6. y=tgx + lnx + 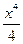 ;
;  =
=
7. y=excosx;  =
=
8. y= 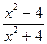 ;
;  =
=
9. y= 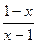 ;
;  =
=
10. y=e3x;  =
=
11. y= x+sinx cosx;  =
=
12. y=sin 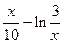 ;
;  =
=
13. y= 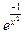 ;
;  =
=
14. y= 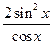 ;
;  =
=
15. y=ln(ecosx);  =
=
16. y= 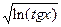 ;
;  =
=
17. y= 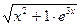 ;
;  =
=
18. y= 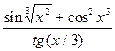 ;
;  =
=
19. y= lg3(x2);  =
=
20. y= 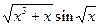 ;
;  =
=
Примеры нахождения дифференциала функции:
1. y= 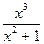 ; dy =
; dy = 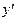 dx;
dx;
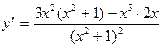 ; dy =
; dy = 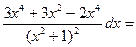
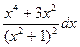 ;
;
2. y= 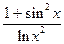 ;
;
dy= 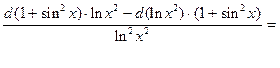
= 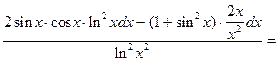 =
= 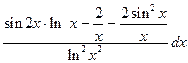 ;
;
Найти дифференциалы следующих функций:
1). y=(2x+x2)3; dy=
2). y= 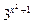 ; dy=
; dy=
3). y= 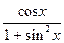 ; dy=
; dy=
4). y=xex-ex-2; dy=
5). y= 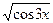 ; dy=
; dy=
Домашнее задание:
I). Найти производные функций:
1). y=(x4-x2+1)3;  =
=
2). y= 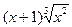 ;
;  =
=
3). y= 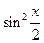 ;
;  =
=
4). y= 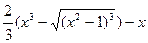 ;
;  =
=
5). y=sin(cos2x)cos(sin2x);  =
=
6). y= 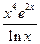 ;
;  =
=
7). y= 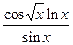 ;
;  =
=
II). Найти дифференциалы функций:
1). y= 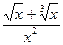 ; dy=
; dy=
2). y=ex/2 cos x/2; dy=
3). y= 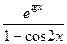 ; dy=
; dy=
Занятие №2.
Тема: Градиент функции. Основы интегрирования.
Цель: 1. Изучение основных понятий и определений. 2. Получение навыков интегрирования. 3. Освоение основных методов интегрирования.
Краткая теория. I. Говорят, что в пространстве задано поле некоторой величины, если в каждой точке пространства определено значение этой величины. Поле может быть скалярным (давление, температура, концентрация) или векторным (скорость, сила).
Поле может быть стационарным, если оно не меняется со временем, или нестационарным в обратном случае. С формальной точки зрения стационарное поле - это функция трех переменных x, y,z:
U (x,y,z). В поле дана точка М. Возможное направление выхода из нее - l.
Производной от U по направлению l называется скорость изменения поля в этом направлении в расчете на единицу длины:
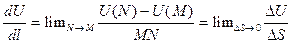 | l
| l
Эту производную можно записать:
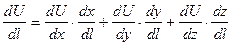
Правую часть удобно записать в виде скалярного произведения двух векторов:
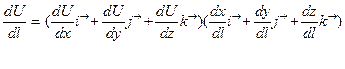
Первый из них называется градиентом поля:
grad U = 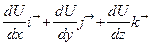 (2.1)
(2.1)
Второй вектор:
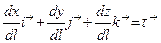
называется единичным вектором направления l.
Вектор grad U в точке М всегда указывает в сторону наибыстрейшего возрастания поля U.
II. Функция F(x), имеющая данную функцию f(x) своей производной или f(x)dx своим дифференциалом, называется первообразной данной функции f(x).
Например: f(x)=cos x ®F(x)=sin x
f(x)= x2 ® F(x)=x3/ 3
Совокупность всех первообразных функций для дифференциала f(x) dx называется неопределенным интегралом и обозначается: 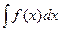 = F(x) + C.
= F(x) + C.
Основные интегралы:
1). 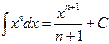 , (n ¹ -1) (2.2); 5).
, (n ¹ -1) (2.2); 5). 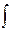 sin x dx= - cos x + C, (2.6);
sin x dx= - cos x + C, (2.6);
2). 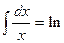 ½x½ + C, (2.3); 6).
½x½ + C, (2.3); 6). 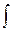 cosx dx= sin x + C, (2.7);
cosx dx= sin x + C, (2.7);
3). 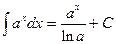 , (2.4); 7).
, (2.4); 7). 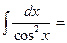 tg x + C, (2.8);
tg x + C, (2.8);
4). 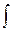 ex dx= ex + C, (2.5); 8).
ex dx= ex + C, (2.5); 8). 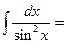 - ctg x + C, (2.9).
- ctg x + C, (2.9).
Основные методы интегрирования.
1. Метод замены переменной.
Если 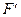 (t) = f(t) и t= j (x), то
(t) = f(t) и t= j (x), то 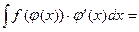 F(j(x)) + C.
F(j(x)) + C.
Например:
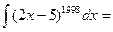 ½d(2x - 5)=2dx ½=
½d(2x - 5)=2dx ½= 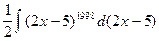 =
=
= 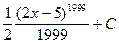
2. Интегрирование подстановкой.
Рассмотрим на примере:
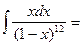
Пусть: 1 - x =t и x=1- t. Дифференцируя имеем: dx= - dt. Тогда:
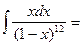 -
- 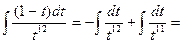
= - 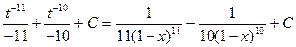 .
.
3. Интегрирование по частям.
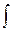 UdV=UV -
UdV=UV - 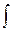 VdU
VdU
Пример:
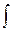 x sinx dx=
x sinx dx= 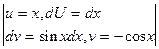 = - x cosx -
= - x cosx - 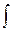 (-cosx)dx= - x× ×cosx+sin x + C.
(-cosx)dx= - x× ×cosx+sin x + C.
Задания для самостоятельного решения и решения у доски.
1). Найти интегралы методом замены переменной.
1). 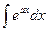 =
=
2). 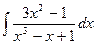 =
=
3). 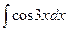 =
=
4). 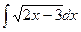 =
=
5). 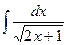 =
=
2). Проинтегрировать методом подстановки:
1. 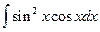 =
=
2. 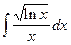 =
=
3. 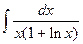 =
=
4.  =
=
5. 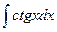 =
=
1. 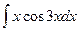 =
=
2. 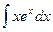 =
=
3. 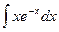 =
=
4. 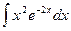 =
=
5. 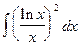 =
=
4). Найдите интегралы:
1. 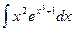 =
=
2. 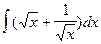 =
=
3. 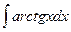 =
=
4. 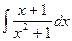 =
=
5. 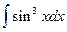 =
=
6. 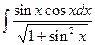 =
=
Домашнее задание.
Вычислить интегралы:
1. 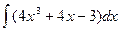 =
=
2. 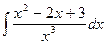 =
=
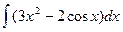 =
=
3). Проинтегрировать по частям.
4.  =
=
5. 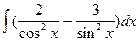 =
=
6. 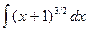 =
=
7. 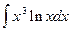 =
=
8. 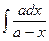 =
=
9. 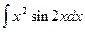 =
=
10. 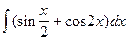 =
=
 2015-04-20
2015-04-20 346
346







