1. Формула Ньютона- Лейбница:
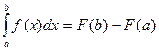 , где (3.1)
, где (3.1)
F(x) - первообразная функции f(x), т.е. 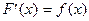 .
.
Свойства определенного интеграла:
 ; (3.2)
; (3.2)
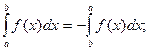 (3.3)
(3.3)
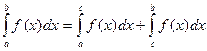 (3.4)
(3.4)
Примеры решения:
1. 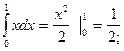
2. 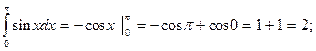
3. 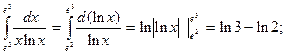
4. 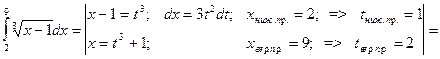
= 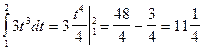 .
.
Обратите внимание, при подстановке пределы интегрирования меняются.
Для вычисления определенного интеграла используются те же методы, что для нахождения неопределенного.
5). Вычислим площадь фигуры, ограниченной линиями:
y=2x - x2 и y=x.
Нужно найти пределы интегрирования a и b. Для этого нужно решить уравнение:
2x - x2 = x
x - x2 = x2 - x = 0
x(x - 1) = 0
x1 = 0 = a
x2 = 1 = b
S= 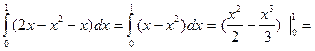 =1/2 - 1/3 = 1/6.
=1/2 - 1/3 = 1/6.
II. Общий вид дифференциального уравнения:
F(x, y, 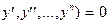 (3.7)
(3.7)
Общее решение дифференциального уравнения:
y=f(x, C1, C2,..., Cn). (3.8)
Общий вид дифференциального уравнения первого порядка:
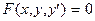 (3.9)
(3.9)
Общее решение дифференциального уравнения первого порядка:
y=f(x, C). (3.10)
1). Дифференциальное уравнение типа 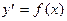 :
:
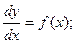 dy=f(x) dx
dy=f(x) dx
Общее решение: y= 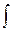 f(x)dx=F(x) + C.
f(x)dx=F(x) + C.
2). Дифференциальное уравнение типа 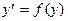 :
:
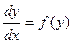 ;
; 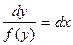
Общее решение: 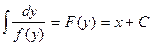
3). Дифференциальное уравнение с разделенными переменными:
f(x) dx + j (y) dy = 0
|
|
|
Общее решение: 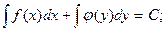
F(x) + F(y) = C.
4). Дифференциальное уравнение с разделяющимися переменными:
f(x) j(y) dx + f(x) Ф(y) dy = 0.
Приведем уравнение к уравнению с разделенными переменными:
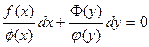
Общее решение: 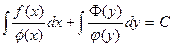 или F1 (x) + F2 (y) = C.
или F1 (x) + F2 (y) = C.
Примеры решения:
1). Является ли решением данного дифференциального уравнения указанная функция?
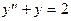 , y=x ex
, y=x ex
Для этого продифференцируем функцию два раза и подставим в исходное уравнение ее вторую производную и саму функцию. Если тождество окажется верным, значит приведенная функция является решением уравнения.
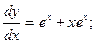
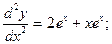 это
это 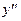
Подставляем в уравнение y и 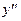 :
:
2 ex + x ex + x ex = 2 ex + 2 x ex ¹ 2
Таким образом, данная функция не является решением приведенного дифференциального уравнения.
2). Найдем общее решение дифференциального уравнения:
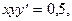
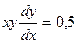
Разделим переменные:

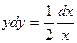
Интегрируем обе части уравнения:
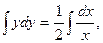
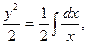
y2 = ln x + C,
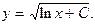 - общее решение.
- общее решение.
Задания для самостоятельного решения и решения у доски.
1). Вычислите интегралы:
1.  =
=
2. 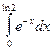 =
=
3. 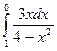 =
=
4. 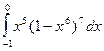 =
=
5. 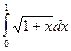 =
=
6. 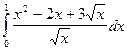 =
=
7. 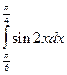 =
=
8. 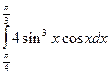 =
=
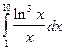 =
=
10. 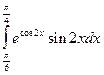 =
=
2. Выясните, является ли решениями данных дифференциальных уравнений указанные функции:
1. 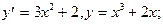
2. 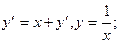
3. 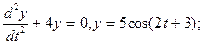
4. 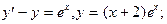
5. (x+2)dx - 2 dy = 0, y=x2 / 4 + x.
3. Найдите общее решение следующих дифференциальных уравнений:
1. 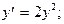
2. (x + 1) dx - 2 xy dy = 0;
3. x dx = y dy;
4. 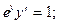
5. 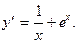
Домашнее задание:
1. Вычислить интегралы:
1). 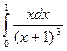 =
= 
2).  =
=
3). 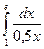 =
=
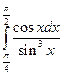 =
=
5). 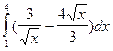
2. Являются ли решениями данных дифференциальных уравнений приведенные функции
1) 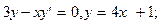
2) 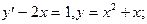
3) 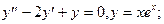
3. Найти общее решение:
1) 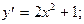
2) 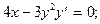
3) dy + 3y dx = 0.
 2015-04-20
2015-04-20 550
550







