Окружная сила на шкивах, Н,
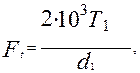 (8)
(8)
где 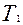 -вращающий момент, Нм, на ведущем шкиве диаметром
-вращающий момент, Нм, на ведущем шкиве диаметром 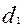 .
.
Из условия равновесия шкива при передаче вращающего момента 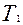 имеем
имеем
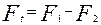 , (9)
, (9)
где  и
и 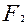 - силы натяжения ведущей и ведомой ветвей ремня под нагрузкой. Так как геометрическая длина ремня от нагрузки не зависит, то можно записать равенство суммарных натяжений ветвей в нагруженной и ненагруженной передаче:
- силы натяжения ведущей и ведомой ветвей ремня под нагрузкой. Так как геометрическая длина ремня от нагрузки не зависит, то можно записать равенство суммарных натяжений ветвей в нагруженной и ненагруженной передаче:
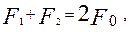 (10)
(10)
где 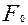 - сила начального натяжения ремня.
- сила начального натяжения ремня.
Из равенств (9) и (10) следует
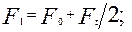
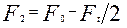 . (11)
. (11)
Сила начального натяжения ремня 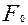 обеспечивает передачу полезной нагрузки за счет сил трения между ремнем и шкивом. С ростом силы
обеспечивает передачу полезной нагрузки за счет сил трения между ремнем и шкивом. С ростом силы 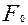 несущая способность ременной передачи возрастает, однако срок службы уменьшается.
несущая способность ременной передачи возрастает, однако срок службы уменьшается.
Уравнения (11) не вскрывают способности передачи передавать нагрузку 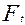 , т.е. тяговой способности передачи.
, т.е. тяговой способности передачи.
Соотношение сил натяжения ведущей и ведомой ветвей ремня определяют по уравнению Эйлера
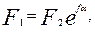 (12)
(12)
где 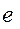 - основание натурального логарифма;
- основание натурального логарифма; 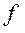 - коэффициент трения;
- коэффициент трения; 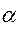 - угол обхвата.
- угол обхвата.
Из формулы (12) видно, что нагрузочная способность ременной передачи возрастает с увеличением 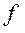 и
и 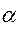 .
.
Нагрузочная способность ременной передачи понижается в результате действия центробежной силы 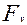 , величина которой определяется по формуле:
, величина которой определяется по формуле:
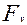 =
= 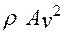 , (13)
, (13)
где 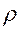 - плотность материала ремня;
- плотность материала ремня; 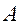 - площадь поперечного сечения ремня.
- площадь поперечного сечения ремня.
Предварительное напряжение 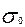 в ремне равно
в ремне равно
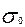 =
= 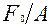 . (14)
. (14)
Полезное напряжение 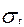 в ремне от окружной силы
в ремне от окружной силы 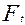 равно
равно
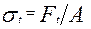 . (15)
. (15)
Напряжения 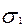 и
и 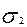 в ветвях ремня от рабочей нагрузки равны
в ветвях ремня от рабочей нагрузки равны
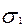 =
= 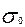 +
+ 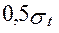 ;
; 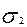 =
= 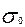 -
- 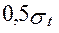 . (16)
. (16)
Напряжения 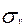 в ремне от действия центробежной силы
в ремне от действия центробежной силы 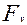 определяется по формуле:
определяется по формуле:
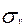 =
= 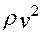
 (17)
(17)
Кроме вышеуказанных напряжений в ремне при обхвате шкивов возникают напряжения изгиба 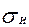 ,которые определяются по формуле
,которые определяются по формуле
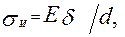 (18)
(18)
где 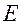 - модуль упругости;
- модуль упругости; 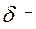 толщина ремня.
толщина ремня.
Суммарное максимальное напряжение в ведущей ветви в месте набегания ремня на малый шкив
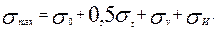 (19)
(19)
Эпюра распределения напряжений по длине ремня показана на рис.3.
Рис.3. Эпюры напряжений в ремне
 2015-05-06
2015-05-06 835
835








