Цепи, не содержащие емкостей и индуктивностей, т.е. энергоемких элементов, называются резистивными. Их математическими моделями являются системы нелинейных уравнений.
В общем случае также уравнения не решаются аналитически. Для их решения используют графоаналитический и численный методы.
Обычно при анализе нелинейных резистивных цепей рассматривают задачу в такой формулировке.
Задана цепь с известными характеристиками НЭ, параметры линейных элементов и параметрами источников постоянного напряжения и тока. Пусть на входе цепи действует один источник переменного сигнала S(t), действующем на входе цепи. Требуется найти реакцию цепи y(t): т.е напряжение или ток на ее входе (1) или выходе (2).
Если сигнал напряжения а отклик ток, то цепь можно рассматривать как двухполюсник (рис. а), если это пара напряжений или пара токов, то как
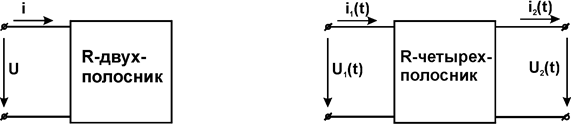
|
четырехполюсник (рис. б).
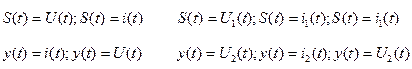
а) б)
Выходной характеристикой резистивного двухполюсника называют зависимость мгновенного значения реакции на входе y(t) от мгновенного значения входного сигнала S(t), т.е. функцию y=y(S). Чаще всего эту функцию называют и передаточной характеристикой резистивного двухполюсника, и определяют последующую зависимость мгновенного значения реакции на выходе y(t) от мгновенного значения входного сигнала S(t), т.е. функцию y(s), т.е. это одно и тоже. Эти характеристики можно измерить экспериментально, подключив в качестве S(t) источник регулируемого напряжения (тока) и регистрируя значения выходной величины в зависимости от входной.
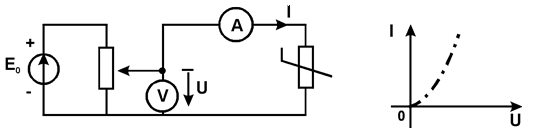
|
На рис. показана схема и результат экспериментального измерения ВАХ НЭ (двухполюсника).
 2015-05-06
2015-05-06 477
477








