2015-05-06
473
Состояние счетчика с произвольным порядком счета с приходом очередного входного сигнала изменяется на величину, отличную от единицы. Исходными данными является порядок перехода счетчика в последующее состояние.
В качестве примера рассмотрим восьмиразрядный счетчик и изменением сначала четных состояний счетчика, а затем нечетных. Таблица функционирований такого счетчика представлена ниже (табл. 5).
Таблица 5
| Состояние счётчика | Функция перехода | ||||||||
| № | Предыдущее | Последующее |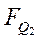 
| 
| 
| ||||
| 
| 
| 
| 
| 
| ||||
| ▲ | |||||||||
| ▲ | ▼ | ||||||||
| ▲ | |||||||||
| ▼ | ▼ | ▲ | |||||||
| ▲ | |||||||||
| ▲ | ▼ | ||||||||
| ▲ | |||||||||
| ▼ | ▼ | ▼ |
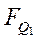
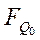
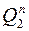
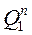
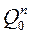
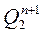
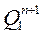
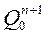
В соответствии с таблицей функционирования счетчика определим функции перехода каждого триггера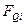 
(см. табл. 5). На основании таблицы переходов триггеров составим карты функций переходов для каждого триггера: 
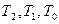(рис. 14).
|
|
|
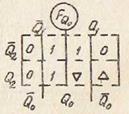
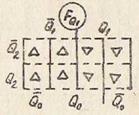
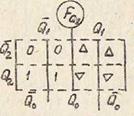
Рис. 14
Заменяя функции переходов в картах, изображенных на рис. 14, значениями функций управления J и K из словаря переходов (см. табл. 2), получаем карты Карно для J и K входов каждого триггера счётчика (рис.15).
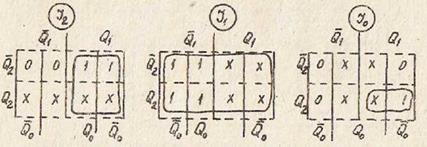
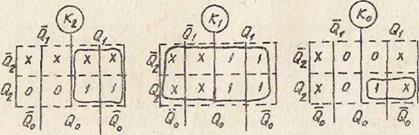
Рис. 15
Минимизируя, получим логические уравнения входов J и K:
; 
; 
.
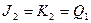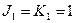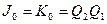Из этих выражений следует, что на J и K входы второго триггера следует подать прямой выход с первого триггера, на J и K входы нулевого триггера - конъюнкцию логических переменных с прямых выходов второго и первого триггеров. На входы первого триггера необходимо подать потенциал соответствующий логической единице.
Схема счетчика, построенного в соответствии с полученными результатами, приведена на рис. 16.
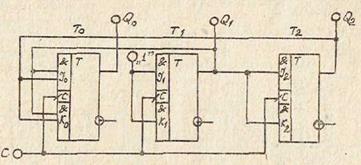
Рис. 16
