Для обобщения данных по рядам динамики рассчитываются:
- средний уровень ряда;
- средний абсолютный прирост;
- средний темп роста и прироста.
Для разных видов рядов динамики средний уровень рассчитывается неодинаково.
По интервальному динамическому ряду из абсолютных величин с равными интервалами средний уровень определяется по средней арифметической простой из уровней ряда:
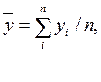
Где yi - уровни ряда для i -го периода; n - число уровней в ряду динамики.
По интервальному временному ряду из относительных и средних величин средний уровень определяется так же, как в статистике, т.е. с учетом информации по признакам, связанным с усредняемым, т.е. по формуле средней арифметической взвешенной:
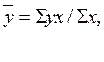
Однако часто в настоящее время при компьютерной обработке данных средний уровень интервального ряда из относительных и средних величин также определяется по средней арифметической простой.
По моментному динамическому ряду в зависимости от исходной информации средний уровень ряда определяется тремя способами.
1. Если известны данные об изменении уровня ряда внутри временного промежутка, то средний уровень определяется как средняя арифметическая взвешенная:
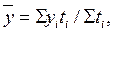
где yi - уровень моментного динамического ряда, ti - период, в течение которого уровень yi остаётся неизменным, т.е. период действия yi..
2. Однако не всегда имеется информация об изменении уровня моментного ряда внутри рассматриваемого временного промежутка. В этом случае средний уровень моментного ряда динамики определяется приближенно как средняя арифметическая взвешенная из парных смежных средних:
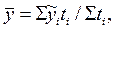
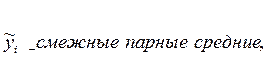
Найденные как средняя арифметическапростая из двух рядом стоящих уровней т.е.
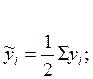
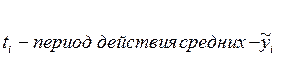
3. Если интервалы между датами равны, то рассмотренная ранее средняя арифметическая взвешенная преобразуется в тождественную ей среднюю хронологическую:
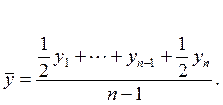
Данная формула используется, например, для расчета среднегодовой стоимости имущества при уплате налога на имущество.
Кроме среднего уровня, при анализе и прогнозировании широко используются средние показатели изменения уровней ряда, а именно средний абсолютный прирост и средний темп роста.
Средний абсолютный прирост определяется как средняя арифметическая простая из цепных приростов:
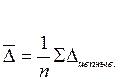
Так как ∑△ цепные= △ базисное, средний абсолютный прирост можно определять следующим образом:
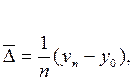
где уп - последний уровень динамического ряда; у0 – уровень, взятый за базу сравнения.
Для обобщения характеристики интенсивности роста рассчитывается средний темп (коэффициент) роста по средней геометрической простой:
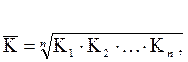
где К1, К2,…Кп – цепные коэффициенты роста; п – число цепных коэффициентов роста.
Среднегодовой темп прироста определяется на основе среднего темпа роста:
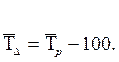
Рассмотренные средние показатели динамики достаточно широко используются при экстраполяции тенденции ввиду их простоты и возможности четко интерпретировать результат.
 2015-05-06
2015-05-06 487
487








