Частотные характеристики стохастического сигнала

Введенная выше автокорреляционная функция 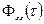описывает временные параметры стохастического сигнала. Преобразовывая ее по Фурье, можно получить адекватное частотное описание стохастического сигнала, Преобразованная по Фурье автокорреляционная функция называется спектральной плот­ностью сигнала и обозначается через :

.

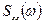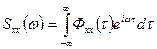Так как 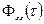представляет собой чётную функцию, то спектральная плотность всегда является чётной и действительной функцией 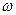. Поэтому эта зависимость идентична следующему:

.

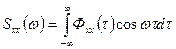Обратное преобразование осуществляют по следующим формулам:

, .

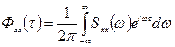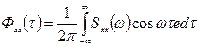Спектральную плотность физически можно интерпретировать как плотность мощности сигнала, распределенную по частотам .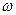

Из последнего соотношения следует:

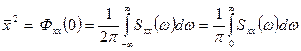. Информация о тенденции к сохра­нению стохастического сигнала, содержащаяся в автокорреля­ционной функции, содержится также и в спектральной плот­ности. Слабая тенденция к поддержанию сигнала означает, что уже при малом смещении времени 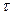величины 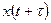и 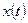становятся некоррелированными. Этому соответствует быстро спадающая с увеличением 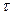автокорреляционная функция. В спек­тральной плотности это проявляется в том, что «мощность» сиг­нала распределена и на высоких частотах. Если сигнал имеет широкочастотный спектр, то он быстро изменяется во времени.