Если учесть сопротивление среды пропорциональное скорости, как это было сделано выше, дифференциальное уравнение колебаний получится таким
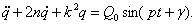 (21)
(21)
Решение его состоит из общего и частного решений. Общее мы уже находили выше. Например, при малом сопротивлении (n < k)
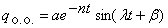 , где
, где 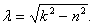
Частное решение будем искать в виде 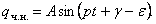 Чтобы определить коэффициенты А и
Чтобы определить коэффициенты А и 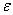 , подставим это решение в уравнение (21). Получим
, подставим это решение в уравнение (21). Получим
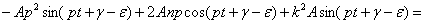
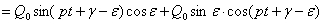
(правую часть уравнения (21) представили как синус суммы двух углов: 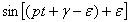 ). Полученное уравнение обратится в тождество, если будут выполнены два условия (сгруппировав члены, содержащие
). Полученное уравнение обратится в тождество, если будут выполнены два условия (сгруппировав члены, содержащие 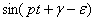 и
и 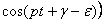 :
:
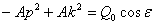 и
и 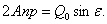
Из этих уравнений получим
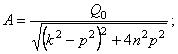
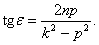 (22)
(22)
Полное решение уравнения (21) будет таким
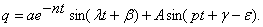 (23)
(23)
Очевидно, за счет сопротивления с течением времени первый член стремится к нулю. Поэтому можно заключить, что установившиеся вынужденные колебания и с учетом сопротивления среды будут гармоническими.
Причем, во-первых, частота колебаний равна частоте изменения возмущающей силы; во-вторых, колебания не зависят от начальных условий и, в-третьих, амплитуда колебаний А зависит от частоты р и от сопротивления среды, характеризующегося коэффициентом n.
График этой зависимости от р и n дан на рис.88.
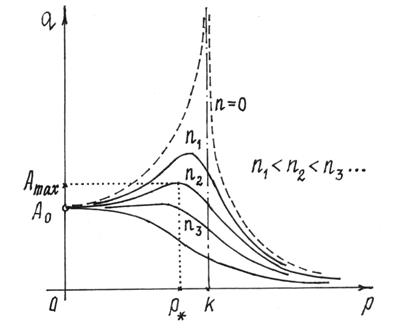
Рис.88
Из графика видно, что при сопротивлении амплитуда колебаний – конечная величина. И максимум амплитуды будет не при p = k, а при несколько меньшей частоте  . Ее можно определить, отыскав максимум амплитуды А или, лучше, минимум функции
. Ее можно определить, отыскав максимум амплитуды А или, лучше, минимум функции 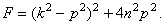
Приравняв к нулю производную, 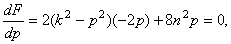 найдем
найдем 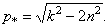 И тогда величина максимальной амплитуды, подставив
И тогда величина максимальной амплитуды, подставив  в (22),
в (22), 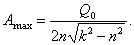
 2015-05-06
2015-05-06 623
623








