Для определения коэффициента трения в данной работе используется метод наклонного маятника (рис. 13.1). Шарик или брусок, подвешенные в точке О, опираются на наклонную плоскость, угол наклона которой к горизонту b можно изменять. Если отклонить маятник от положения равновесия на угол a0, то он начнет совершать затухающие колебания. В результате за n колебаний угол отклонения уменьшится до значения 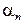 . Затухание колебаний происходит главным образом под действием внешнего трения.
. Затухание колебаний происходит главным образом под действием внешнего трения.
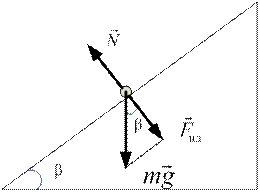
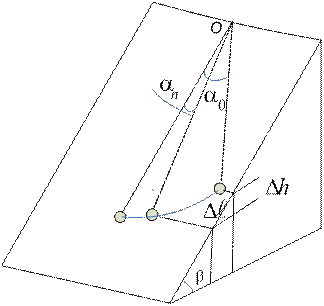
а б
Рис. 13.1
Коэффициент трения скольжения 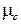 равен отношению силы трения
равен отношению силы трения 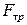 к силе реакции опоры N (которая, согласно III закону Ньютона, всегда равна силе нормального давления
к силе реакции опоры N (которая, согласно III закону Ньютона, всегда равна силе нормального давления 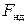 , прижимающей тело к опоре)
, прижимающей тело к опоре)
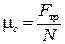 . (13.1)
. (13.1)
В рассматриваемом случае (рис. 13.1а) сила реакции опоры по модулю равна составляющей силы тяжести 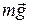 , направленной перпендикулярно плоскости
, направленной перпендикулярно плоскости
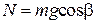 , (13.2)
, (13.2)
где m – масса маятника, g – ускорение свободного падения.
Сила трения может быть найдена с помощью закона сохранения энергии. Согласно которому работа, совершенная силой трения за n колебаний, равна изменению потенциальной энергии тела за то же число колебаний
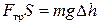 , (13.3)
, (13.3)
где 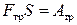 – работа силы трения, S – расстояние, пройденное телом за n колебаний,
– работа силы трения, S – расстояние, пройденное телом за n колебаний, 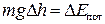 – изменение потенциальной энергии тела за то же число колебаний, D h – изменение высоты тела вследствие затухания колебаний.
– изменение потенциальной энергии тела за то же число колебаний, D h – изменение высоты тела вследствие затухания колебаний.
С учетом формул (13.2) и (13.3) формула (13.1) принимает вид
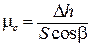 . (13.4)
. (13.4)
Далее, из рис. 13.1б видно, что
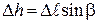 , (13.5)
, (13.5)
где 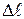 – расстояние между начальным и конечным положениями тела, отсчитанное по наклонной плоскости.
– расстояние между начальным и конечным положениями тела, отсчитанное по наклонной плоскости.
Подставив (13.5) в (13.4), получим для коэффициента трения скольжения формулу
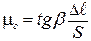 . (13.6)
. (13.6)
Теперь осталось выразить величины 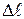 и
и 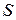 через величины, измеряемые на опыте: число колебаний и углы отклонения маятника от положения равновесия
через величины, измеряемые на опыте: число колебаний и углы отклонения маятника от положения равновесия 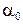 и
и 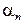 . Рис. (13.2) поясняет, как это можно сделать.
. Рис. (13.2) поясняет, как это можно сделать.
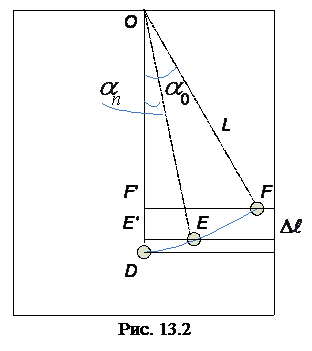 На рисунке изображены три положения тела: положение равновесия D, начальное положение F, соответствующее отклонению на угол
На рисунке изображены три положения тела: положение равновесия D, начальное положение F, соответствующее отклонению на угол 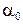 , и конечное положение E, соответствующее отклонению на угол
, и конечное положение E, соответствующее отклонению на угол 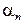 . Из рис. 13.2 видно, что
. Из рис. 13.2 видно, что 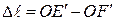 .
. 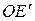 и
и 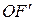 можно представить через длину нити маятника L и углы его отклонения от положения равновесия. Действительно, из треугольника EOE ¢ следует, что
можно представить через длину нити маятника L и углы его отклонения от положения равновесия. Действительно, из треугольника EOE ¢ следует, что 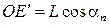 , а из треугольника FOF¢ –
, а из треугольника FOF¢ – 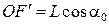 . Итак,
. Итак,
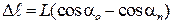 .
.
Если учесть, что при малых углах 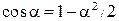 то
то 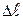 можно представить в виде
можно представить в виде
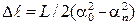 . (13.7)
. (13.7)
Путь S, пройденный телом, можно найти, руководствуясь следующими соображениями. За одно полное колебание тело проходит расстояние, равное четырем амплитудам 4 A. За n колебаний пройденный путь S = 4 nA. Но амплитуда вследствие затухания изменяется от начального значения А 0, равного дуге DF, до конечного значения A n, равного дуге DE, поэтому надо взять ее среднее значение. Из рис. 13.2б видно, что А 0 » a0 L, а A n » an L (здесь углы выражены в радианах), следовательно, среднее значение амплитуды равно L (a0 + an)/2. Итак,
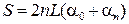 . (13.8)
. (13.8)
Подставив (13.7) и (13.8) в (13.6), получим формулу для расчета коэффициента трения скольжения в данной работе
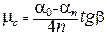 . (13.9)
. (13.9)
 2015-05-06
2015-05-06 536
536








