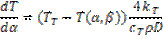Тема: составление математической модели динамики объекта с распределенными координатами и получение статических характеристик на ЭВМ

Лабораторная работа 7

Цель: приобрести навыки моделирования динамики объектов с распределенными координатами, произвести численное решение уравнений динамики и получить динамические характеристики объекта с распределенными параметрами на ЭВМ.

Общие положения.

Объекты с распределенными координатами характеризуются изменением технологических координат (температуры, концентрации, плотности и т.д.) по длине, радиусу, и для их описания используются гидродинамические модели «идеального вытеснения», диффузионные, ячеечные и др.

Динамический режим работы объекта характеризуется изменением выходных координат при изменении входных или при воздействии возмущений.

При описании процессов, протекающих в объектах с распределенными координатами в динамическом режиме, необходимо учитывать изменение концентрации, температуры и других координат во времени, по длине, радиусу. В связи с этим математическая модель динамики объекта с распределенными координатами представляет собой систему уравнений в частных производных – наиболее сложный случай при моделировании технологических объектов.

Для решения уравнения в частных производных могут использоваться методы конечных элементов, конечных разностей, метод сведения к обыкновенным дифференциальным уравнениям с параметром (метод характеристик).

Геометрическое построение динамической характеристики объекта с распределенными координатами возможно лишь в простейшем случае, когда дифференциальное уравнение включает только две частные производные.

В качестве примера в данной лабораторной работе будет рассмотрено моделирование динамики процесса нагревания жидкости в трубчатом теплообменнике.

Трубчатый теплообменник (рисунок 1) представляет собой пучок труб, помещенных в кожух, по которым движется нагреваемая жидкость. В межтрубном пространстве движется теплоноситель. При движении по трубам жидкость нагревается за счет тепла, поступающего от теплоносителя. Движущей силой процесса является разность температур нагреваемой жидкости и теплоносителя.

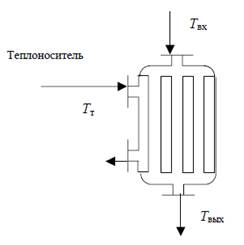
Рисунок 1 – Конструкция трубчатого теплообменника

Входными координатами данного объекта являются температура Т_вх нагреваемой жидкости на входе в теплообменник; температура Т_τ теплоносителя; скорость u движения жидкости по трубам. Выжодная координата – температура Т (τ,l) в любой момент времени τ и в любом сечении, находящемся на расстоянии l от начала трубы.

Для получения математической модели выбранного объекта рассмотрим в качестве звена обну трубу теплообменника.

Примем следующие допущения:

1. Движение нагреваемой жижкости в трубе описывается гидродинамической моделью «идеального вытеснения».

2. Температура теплоносителя Т_τ постоянна по длине трубы и во времени.

3. Коэффициент теплопередачи k_τ не меняется по длине трубы.

4. Плотность ρ и теплоемкость С_t нагреваемой жидкости постоянны.

С учетом принятых допущений математическую модель динамики трубчатого теплообменника можно записать в следующем виде:

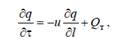(1)

где ∂q – изменение количества тепла нагшреваемой жидкости; Q_т – количество тепла, поступающее к жидкости от теплоносителя.

Выразим ∂q через изменение температуры ∂Т нагреваемой жидкости:

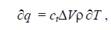(2)

где с_t - теплоемкость нагреваемой жидкости; ρ – плотность нагреваемой жидкости: ΔV – объем нагреваемой жидкости.

Аналогично выразим через Т тепло Q_т.

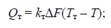(3)

Здесь k_τ – коэффициент теплопередачи; ΔF – площадь поверхности теплообмена; Т_τ – температура теплоносителя.

Подставим зависимости (1) и (2) в уравнение (1):

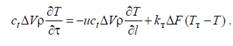(3)

Выразим ΔV и ΔF черездлину трубы Δl и диаметр D трубы:

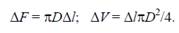(4)

Окончательно получаем:

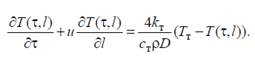(5)

Коравые условия Т(0, l)=T₀(l); T(τ, 0)=T_вх(τ).

Область определения независимых переменных: 0 ≤ l ≤ L, где L – длина трубы реактора.

Для решения дифференциального уравнения (5) будем использовать метод сведения к обыкновенным дифференциальным уравнениям с параметром, называемый также методом характеристик.

Заменим τ и l через α и β:

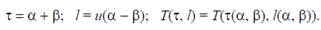(6)

В результате получаем обыкновенное дифференциальное уравнение вида:

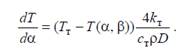(7)

Уравнение (7) полностью эквивалентно уравнению (6). Преобразуем области построения независимых переменных:

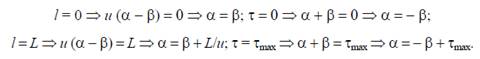
Начальное условие Т₀(l), будет при α = β:

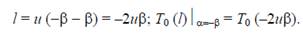(8)

Граничное условие Т_вх(τ) при α = β:

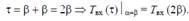(9)

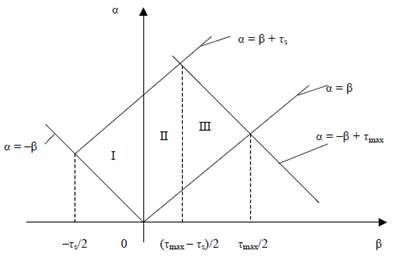
Рисунок 2 – Области построение независимых пиеременных и кравые условия: τ_s = L/u - среднее время пребывания/

В результате получили три области, отличающиеся краевыми условиями (рисунок 2).

I. Область определения β є [-τ_s/2, 0]:

1. Начинать интегрирование в уравнения (7) со значениями α = -β;

2. За начальное условие для уравнения (7) взять Т₀(-2uβ);

3. Заканчивать интегрирование при условии α = β +τ_s

II. Область определения β є [0, (τ_max -τ_s)/2]:

1. Начинать интегрирование в уравнения (7) со значениями α = β;

2. За начальное условие для уравнения (7) взять Т_вх(2β);

3. Заканчивать интегрирование при условии α = β +τ_s

III. Область определения β є [(τ_max -τ_s)/2, τ_max/2]:

1. Начинать интегрирование в уравнения (7) со значениями α = β;

2. За начальное условие для уравнения (7) взять Т_вх(2β);

3. Заканчивать интегрирование при условии α = -β +τ_max.

Порядок выполнения работы.

1. Составить блок-схему алгоритма решения уравнения (7) для трех областей определения независимых переменных α и β.

2. Выполнить необходимые расчеты используя Excel Microsoft.

3. Получить динамическую характеристику трубчатого теплообменника и построить ее в виде графика в координатах Т, τ, l.

Постоянные величины, необходимые для расчета:

k_τ = 6500 Вт/м₂·град;

с_t =4190 Дж/кг·град;

ρ = 1000 кг/м³;

Т_τ = 80 °С;

L = 1 м;

D = 0,05 м;

u = 0,2 м/с;

τ_max = 10 с

Краевые условия для исходного уравнения (6) приведены в индивидуальном задании. Краевые условия необходимо преобразовать согласно методике, приведенной выше.

При интегрировании использовать следующие значения шага переменных: Δα = 0,3; Δβ = 0,2.

Содержание отчета:

1. Выполненные расчеты

ФИО

вариант 1

ПЗ константы                   kt ct ρ Tt L D u τmax Δα Δβ Вт/кв.м*град Дж/кг/град кг/кубм град м м м/с с               0,05 0,2   0,3 0,2

исходные данные
Т0(l)	Твх(τ)
10+10l	20+5sinτ
	математическая модель динамики трубчатого аппарата
	краевые условия
	Т(0,l)=T0(l)
	T(τ,0)=Tвх(τ)

№п/п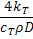

Δα

Δβ

Δl

T0(l)

Т(0,l)

F(0,l)

Δτ

Tвх(τ)

T(τ,0)

F(τ,0)

2. Графики полученных зависимостей Т (τ, l),

Контрольные вопросы

1. Какие численные методы используются для решения уравнений, описывающих динамические режимы работы объектов с распределенными координатами? Дать сравнительную характеристику методов.

2. Как изменится математическая модель трубчатого теплообменника при отмене допущения о постоянстве температуры теплоносителя по длине теплообменника и по времени?