Необходимым условием регулирования рыночных отношений является составление надежных прогнозов развития социально-экономических явлений.
Выявление и характеристика трендов и моделей взаимосвязи создают базу для прогнозирования, т. е. для определения ориентировочных размеров явлений в будущем. Для этого используют метод экстраполяции.
Экстраполяция это нахождение уровней за пределами изучаемого ряда, т. е. продление в будущее тенденции, наблюдавшейся в прошлом (перспективная экстраполяция). Поскольку в действительности тенденция развития не остается неизменной, то данные, получаемые путем экстраполяции ряда, следует рассматривать как вероятностные оценки.
Экстраполяцию рядов динамики осуществляют различными способами, например, экстраполируют ряды динамики выравниванием по аналитическим формулам. Зная уравнение для теоретических уровней и подставляя в него значения t за пределами исследованного ряда, рассчитывают для t вероятностные 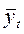 .
.
На практике результат экстраполяции прогнозируемых явлений обычно получают не точечными (дискретными), а интервальными оценками.
Для определения границ интервалов используют формулу:
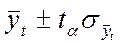
tα— коэффициент доверия по распределению Стьюдента;
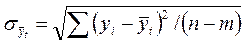 - остаточное среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы (п - т);
- остаточное среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы (п - т);
п — число уровней ряда динамики;
т — число параметров адекватной модели тренда (для уравнения
прямой т = 2). Вероятностные границы интервала прогнозируемого явления:
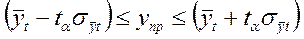
Нужно иметь в виду, что экстраполяция в рядах динамики носит не только приближенный, но и условный характер.
Число степеней свободы — число элементов статистической совокупности, вариация которых свободна (неограничена).
Стьюдент — псевдоним английского математика и статистика Уильяма С. Госсета, разработавшего метод статистических оценок и проверки гипотез t-распределения, не являющегося нормальным.
РЕГРЕССИОННЫЙ АНАЛИЗ СВЯЗНЫХ ДИНАМИЧЕСКИХ РЯДОВ
Многомерные временные ряды, показывающие зависимость результативного признака от одного или нескольких факторных, называют связными рядами динамики. Применение методов наименьших квадратов для обработки рядов динамики не требует предположений о законах распределения исходных данных. Но при использовании метода наименьших квадратов для обработки связных рядов надо учитывать наличие автокорреляции (авторегрессии), которая не учитывалась при обработке одномерных рядов динамики, поскольку ее наличие способствовало более плотному и четкому выявлению тенденции развития рассматриваемого социально-экономического явления во времени.
В значительной части рядов динамики экономических процессов между уровнями существует взаимосвязь. Ее можно представить в виде корреляционной зависимости между рядами у 1, у2, у3,…уn и этим же рядом сдвинутым относительно первоначального положения на h моментов времени y 1+ h, y 2+h, y3+h …y n+h. Временное смещение L называется сдвигом, а само явление взаимосвязи - автокорреляцией.
Автокорреляционная зависимость существенна между последующими и предшествующими уровнями ряда динамики.
При анализе нескольких взаимосвязанных рядов динамики важно установить наличие и степень их автокорреляции(поскольку классические методы математической статистики применимы лишь в случае независимости отдельных членов ряда между собой).
Различаются два вида автокорреляции:
1) автокорреляция в наблюдениях за одной или более переменными;
2) автокорреляция ошибок или автокорреляция в отклонениях от тренда.
Наличие последней приводит к искажению величин средних квадратических ошибок коэффициентов регрессии, что затрудняет построение доверительных интервалов для коэффициентов регрессии, а также проверку их значимости.
Автокорреляцию измеряют при помощи нециклического коэффициента автокорреляции, который рассчитывается не только между соседними уровнями, т. е. сдвинутыми на один период, но и между сдвинутыми на любое число единиц времени (L). Этот сдвиг, именуемый временным лагом, определяет и порядок коэффициентов автокорреляции: первого порядка (при L = 1), второго порядка (при L = 2) и т.д.
Формулу коэффициента автокорреляции можно записать следующим образом:
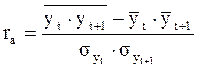
где 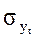 ,
, 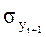 - среднее квадратическое отклонение рядов уt и уt+1 соответственно.
- среднее квадратическое отклонение рядов уt и уt+1 соответственно.
Если значение последнего уровня (уn) ряда мало отличается от первого (у1), то сдвинутый ряд не укорачивается, его можно условно дополнить, принимая уn = у1. Тогда уt = уt+1 и 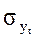 =
= 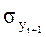 , поскольку рассчитываются они для одного и того же ряда. При такой замене, т. е. если
, поскольку рассчитываются они для одного и того же ряда. При такой замене, т. е. если 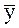 t
t 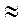
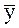 t+1 и
t+1 и 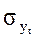
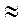
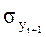 ,формула коэффициента автокорреляции примет вид:
,формула коэффициента автокорреляции примет вид:
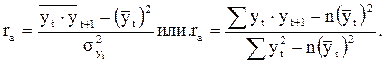
Если ряд динамики состоит из уровней, среднее значение вторых равно нулю (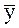 = 0), то выражение yпрощается:
= 0), то выражение yпрощается:
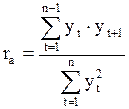 .
.
Для суждения о наличии или отсутствии автокорреляции в исследуемом ряду фактическое значение коэффициентов автокорреляции сопоставляется с табличным (критическим) для 5%-ного или 1%-ного уровня значимости (вероятности допустить ошибку при принятии нулевой гипотезы о независимости уровней ряда).
(Одна из специальных таблиц, в которой определена критическая область проверяемой гипотезы (об отсутствии автокорреляции), составленная Р. Андерсеном в 1942 г., приведена в приложении 12.)
Если фактическое значение коэффициента автокорреляции меньше табличного, то гипотеза об отсутствии автокорреляции в ряду может быть принята. Когда же фактическое значение больше табличного, можно сделать вывод о наличии автокорреляции в ряду динамики.
Для уменьшения автокорреляции применяют различные методы. Bсе они преследуют цель исключения основной тенденции (тренда) из первоначальных данных.
Самым распространенным примером выявления наличия автокорреляции в отклонениях от тренда или от регрессионной модели является использование критерия Дарбина - Уотсона, который рассчитывается по формуле
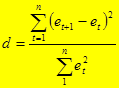
где еt = уt - 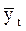 .
.
Теоретическое основание применения этого критерия обусловлено тем, что в динамических рядах как сами наблюдения, так и отклонения от них распределяются в хронологическом порядке.
При условии, что отклонения уровней от тенденции (так называемые остатки) случайны, значения D, лежащие в интервале 0 - 4, всегда будут находиться ближе к 2. Если автокорреляция положительная, то D < 2; отрицательная - 2< = D < = 4. Следовательно, оценки, получаемые по критерию, являются не точечными, а интервальными. Их значения для трех уровней значимости (α = 0,01, α= 0,025 и α = 0,05) с учетом числа наблюдений даны в специальных таблицах.
Существует ряд способов исключения или уменьшения автокорреляции (авторегрессии) в рядах динамики:
а) метод включения времени в качестве дополнительного фактора;
б) метод последовательных разностей;
в) метод авторегрессионных преобразований.
Рассмотрим эти способы исключения автокорреляции (авторегрессии).
В соответствии с теоремой, доказанной Фришем и Boy, время вводится в систему связных динамических рядов в явной форме в качестве дополнительного фактора. Уровни исходных динамических рядов могут быть представлены показателями в любой форме, в том числе логарифмической, а время всегда вводится в линейной форме. Считается, что введение фактора времени исключает основную тенденцию развития всех явлений, представленных исследуемыми рядами динамики. Доказано, что введение времени аналогично использованию отклонения фактических данных от трендов.
Применение метода наименьших квадратов к обработке многомерных временных рядов не отличается от методологии применения его к обычным статистическим рядам. В рассматриваемом случае минимизируется следующее выражение:
S = 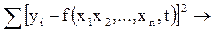 min.
min.
При исключении автокорреляции методом последовательных разностей
обработке методом наименьших квадратов подвергаются не сами уровни исходных рядов уt, yt+1,..., Уt+n, и хt, хt+1,..., xt+n, а последовательные разности между ними:
Δy1=yt-yt-1; Δxt=xt-xt-1;
Δy2=yt-1-yt-2; Δx2=xt-1-xt-2;
…………… …………….
…………… …………….
Δyk=yt-k-yt-k-1; Δxk=xt-k-xt-k-1.
При использовании этого метода исходят из того, что все разности между уровнями динамических рядов, начиная с первой, будут содержать только случайную компоненту. Причем первые разности содержат случайную компоненту в линейной форме, вторые - описываемую параболой второго порядка, третьи - показательной функцией.
Метод авторегрессионных преобразований заключается в том, что определяют уравнение связи между отклонениями от тенденций двух связных рядов динамики:

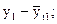

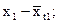
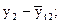
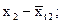
…………. ………….
………… ………….
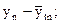
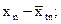
В этом случае также получают уравнения регрессии, не искаженные влиянием автокорреляции.
Введение времени в качестве дополнительной переменной является наиболее действенным способом обработки связных рядов динамики. При линейной связи между исследуемыми рядами этот способ более точен, чем использование последовательных разностей или отклонений от трендов.
При обработке методом наименьших квадратов последовательных разностей или отклонений от трендов обрабатываются чисто случайные величины.
КОРРЕЛЯЦИЯ РЯДОВ ДИНАМИКИ
При изучении развития явления во времени возникает необходимость оценить степень взаимосвязи в изменениях уровней двух или более рядов динамики различного содержания, но связанных между собой. Эта задача решается методами коррелирования:
1) уровней ряда динамики;
2) отклонений фактических уровней от тренда;
3) последовательных разностей, т. е. путем исчисления парного коэффициента корреляции.
Коррелирование уровней ряда динамики правильно показывает тесноту связи между рядами динамики лишь в том случае, если в каждом из них отсутствует автокорреляция.
В этом случае величину коэффициента корреляции находят по формуле
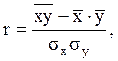
где хi - уровни факторного ряда динамики;
уi - уровни результативного ряда динамики.
Следовательно, прежде чем коррелировать ряды динамики (по уровням), необходимо проверить каждый из рядов на наличие или отсутствие в них автокорреляции (при помощи коэффициента автокорреляции). В случае наличия автокорреляции между уровнями ряда последняя должна быть устранена.
Рассмотрим способы ее исключения в рядах динамики. Коррелирование отклонений от выравненных уровней (тренда). Этот способ состоит в том, что коррелируют не сами уровни, а отклонения фактических уровней от выравненных, отражающих тренд, т. е. коррелируют остаточные величины. Для этого каждый ряд динамики выравнивают по определенной, характерной для него аналитической формуле, затем из эмпирических уровней вычитают выравненные (т. е. находят dx = хt - 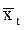 ;dy = уt -
;dy = уt - 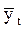 ;) и определяют тесноту связи между рассчитанными отклонениями (dx и dy) по формуле
;) и определяют тесноту связи между рассчитанными отклонениями (dx и dy) по формуле
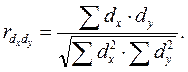
Коррелирование последовательных разностей. Исключить влияние автокорреляции можно путем вычитания из каждого уровня предшествующего ему, т. е. находя разности уровней (уi – у i-1).При переходе от уровней к их разностям исключается влияние общей тенденции на колеблемость. При этом при изменении уровней по прямой можно коррелировать первые разности, при изменении по параболе n-го порядка - n-е разности. Формула коэффициента разностей, используемая для измерения тесноты связи между исследуемыми рядами, имеет вид:
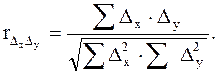
Коэффициент корреляции, рассчитанный для измерения тесноты зависимости изменения уровней двух рядов, является средним, обобщающим показателем. Однако для длительного периода эта зависимость может меняться во времени. Поэтому чтобы судить о том, в какие периоды зависимость между изменениями уровней двух рядов слабая или сильная, надо рассчитывать серию скользящих коэффициентов корреляции для определенного интервала времени.
 2015-05-06
2015-05-06 1971
1971
