Разложение в ряд Котельникова

Этот тип разложения применяется для описания сигналов с ограниченным спектром, т. е. сигналов, спектр которых тождественно равен нулю на частотах выше некоторой граничной частоты w _в.

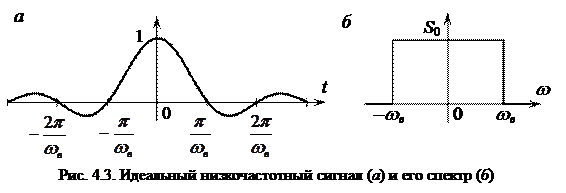В основу построения базисных функций ряда Котельникова положен так называемый идеальный низкочастотный сигнал, спектральная плотность которого постоянна в области частот от – w _в до w _в и равна нулю за пределами этой области (см. рис. 4.3, а). Соответствующая временная зависимость может быть найдена посредством применения обратного преобразования Фурье к спектральной плотности (рис. 4.3, б):

u 0(t)

.

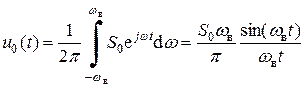Обычно величина S ₀ выбирается равной p/ w _в, тогда выражение для временной зависимости идеального низкочастотного сигнала имеет максимально простой вид:

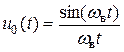. (4.12)

Базис ряда Котельникова образуют функции вида (4.12), смещенные на величину Т = p/ w _в, т. е.

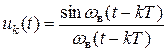. (4.13)

Здесь k может принимать любые целочисленные значения от –¥ до +¥. Интервал Т = p/ w _в, характеризующий взаимное смещение базисных функций, называется интервалом Найквиста.

Для дальнейшего анализа нам нужно определить спектральные плотности базисных функций u_k (t). Поскольку спектральная плотность идеального низкочастотного сигнала нам известна, а базисные функции u_k (t) отличаются от него лишь смещением во времени, применим теорему о запаздывании и, учитывая, что S ₀ = p/ w _в = Т, получаем:

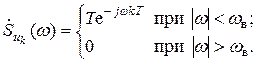(4.14)

Докажем, что базисные функции u_k (t) ортогональны. Для этого воспользуемся равенством Парсеваля (2.53):

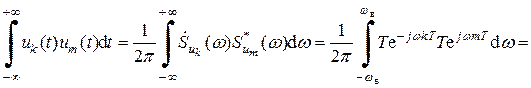
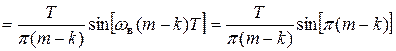. (4.15)

Отсюда следует, что при m ¹ k сигналы u_k (t) и u_m (t) ортогональны.

Норму сигнала u_k (t) можно найти из (4.15), положив m = k. Нетрудно убедиться, что

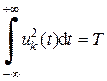. (4.16)

Теперь рассмотрим разложение произвольного сигнала f (t) в ряд по функциям (4.13):

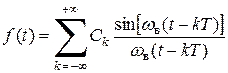. (4.17)

Поскольку норма базисных функций (4.13) не равна 1, для вычисления коэффициентов C_k воспользуемся формулой (4.3):

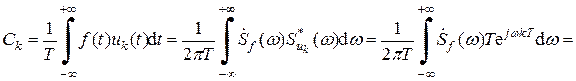
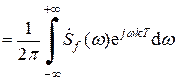. (4.19)

Выражение (4.19) совпадает с формулой обратного преобразования Фурье для сигнала f (t) при t = kT. Следовательно,

C_k = f (kT), (4.20)

т. е. коэффициенты разложения произвольного сигнала f (t) с ограниченным спектром в ряд (4.17) равны значениям сигнала f (kT), и формулу (4.17) можно переписать в виде:

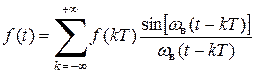. (4.21)

Формула (4.21) представляет собой математическое выражение известной теоремы В.А. Котельникова (теоремы отсчетов), которая формулируется следующим образом: сигнал, в спектре которого не содержатся частоты выше w_в, может быть полностью описан своими дискретными значениями, взятыми с интервалом Т = p/w_в.

Описание сигнала с помощью ряда В.А. Котельникова можно проиллюстрировать с помощью рис. 4.4, где полужирной линией показана функция f (t), а тонкими линиями – составляющие ряда Котельникова, т. е. функции 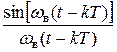, умноженные на значения f (kT).

Если просуммировать все составляющие ряда, то получится в точности функция f (t). Если спектр сигнала не содержит составляющих с частотой выше w _в, то любое промежуточное значение сигнала может быть однозначно и точно восстановлено с помощью ряда (4.21) по своим отсчетным значениям f (0), f (Т), f (2 Т), …, f (kT), ….

Теорема В.А. Котельникова играет ключевую роль в дискретной и цифровой обработке сигналов, позволяя правильно выбрать интервал дискретизации сигнала перед последующей обработкой.