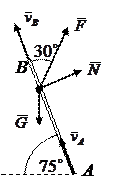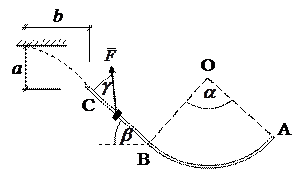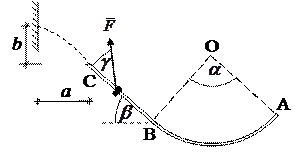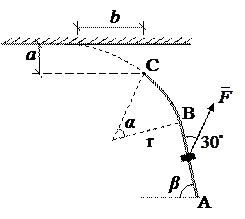 |
| Рис.1.1. Условие задачи | 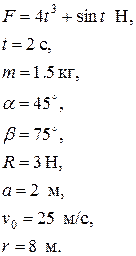
|
| Найти расстояние b и давление шайбы на ось в точке С. |
Решение. Для того, чтобы определить b, надо знать скорость шайбы в точке С. Для этого необходимо сначала рассмотреть движение шайбы по прямолинейному участку пути АВ, а затем по криволинейному ВС.
а) Участок АВ
Рис.1.2. Участок АВ |
Изобразим действующие на шайбу силы. В проекции на ось АВ запишем уравнение теоремы об изменении количества движения (G = mg)
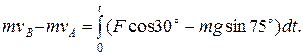 Отсюда найдем скорость шайбы в точке В
(vА = v0)
Отсюда найдем скорость шайбы в точке В
(vА = v0)
| |||
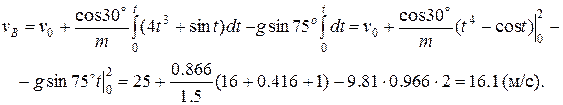
|
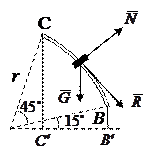 б) Участок ВС
б) Участок ВС
| Найдем работу сил, приложенных к шайбе, на участке пути ВС. Сила тяжести совершает работу на перепаде высот между точками С и В. Так как точка перемещается вверх, то работа должна быть меньше нуля. Из чертежа ясно, что работа равна | Рис. 1.3. Участок ВС | ||||
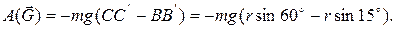 Сила трения направлена по касательной к траектории, длина пути (дуга ВС) равна
Сила трения направлена по касательной к траектории, длина пути (дуга ВС) равна 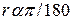 , где , где 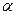 – угол в градусах. Теорема об изменении кинетической энергии точки на участке ВС примет вид – угол в градусах. Теорема об изменении кинетической энергии точки на участке ВС примет вид
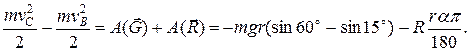 Отсюда найдём
Отсюда найдём
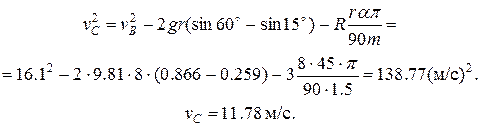
| |||||
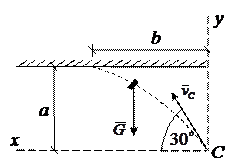 в) Участок свободного полета
Рис.1.4. Участок свободного полёта в) Участок свободного полета
Рис.1.4. Участок свободного полёта
| |||||
Составим уравнение движения тела, брошенного под углом 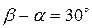 к горизонту с начальной скоростью к горизонту с начальной скоростью 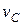 . Начало координат поместим в точке С. Время t будем отсчитывать от нуля. На шайбу действует только одна сила – вертикальная сила тяжести . Начало координат поместим в точке С. Время t будем отсчитывать от нуля. На шайбу действует только одна сила – вертикальная сила тяжести 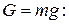
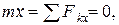 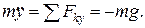 Проинтегрируем эти уравнения дважды при начальных условиях
Проинтегрируем эти уравнения дважды при начальных условиях
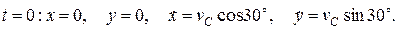
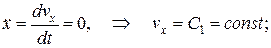
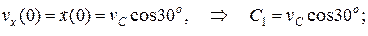
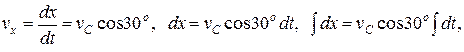
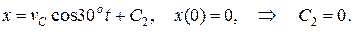 Окончательно
Окончательно 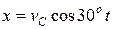 . .
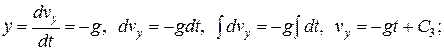
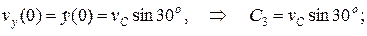
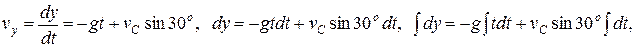
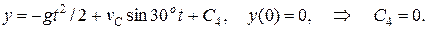 Окончательно
Окончательно 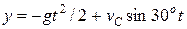 .
В некоторый момент .
В некоторый момент 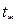 шайба ударится о преграду на высоте y = a. Найдем шайба ударится о преграду на высоте y = a. Найдем 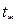 , решив квадратное уравнение , решив квадратное уравнение 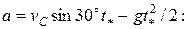
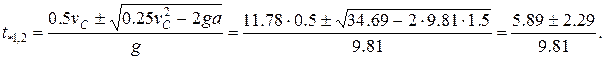
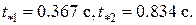 Из двух решений берем меньшее – момент первого пересечения траектории с поверхностью преграды. При
Из двух решений берем меньшее – момент первого пересечения траектории с поверхностью преграды. При 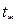 = 0.367 имеем = 0.367 имеем
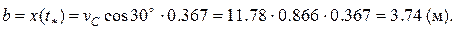 Найдем давление шайбы на ось в точке С, применив принцип Даламбера. Изобразим действующие на шайбу силы и добавим силы инерции (рис. 1.5).
Найдем давление шайбы на ось в точке С, применив принцип Даламбера. Изобразим действующие на шайбу силы и добавим силы инерции (рис. 1.5).
| |||||
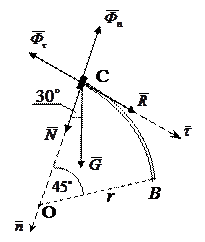  Рис.1.5. Силы, действующие на шайбу в точке С
Рис.1.5. Силы, действующие на шайбу в точке С
| Спроецируем силы на ось главной нормали к траектории движения 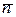 , направленную от С к О. Согласно принципу Даламбера, сумма проекций должна быть равна нулю: , направленную от С к О. Согласно принципу Даламбера, сумма проекций должна быть равна нулю:
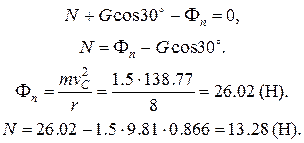
 – это реакция опоры, следовательно, сила давления шайбы на ось равна 13.28 Н и направлена вверх. – это реакция опоры, следовательно, сила давления шайбы на ось равна 13.28 Н и направлена вверх.
| ||||
Ответ: b = 4.74 м, N = 13.28 Н.
Таблица 1.1
Варианты рисунков к задаче Д1 (предпоследняя цифра шифра)
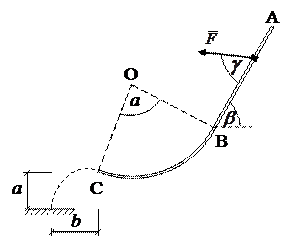 Рис. 0
Рис. 0
| 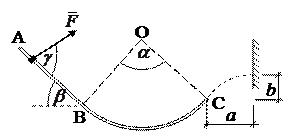 Рис. 1
Рис. 1
| ||||||||||
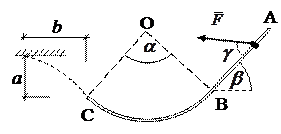 Рис. 2
Рис. 2
| 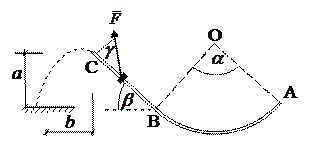 Рис. 3
Рис. 3
| ||||||||||
Рис. 4 | Рис. 5 | ||||||||||
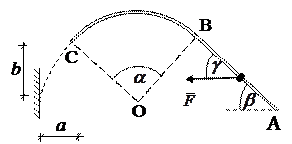 Рис. 6
Рис. 6
| 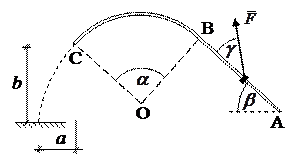 Рис. 7
Рис. 7
| ||||||||||
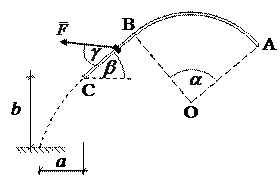 Рис. 8
Рис. 8
|
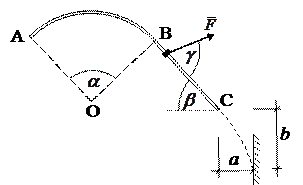 Рис. 9
Рис. 9
|
Таблица 1.2
Исходные данные к задаче Д1
| Последняя цифра шифра | 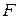 Н
Н
| 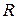 Н
Н
| 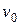 м/с
м/с
| 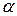 град
град
|  град
град
| 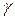 град
град
| m кг | t1 c | а м |
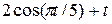
| 0.5 | ||||||||
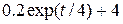
| 0.2 | ||||||||
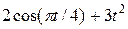
| 0.9 | ||||||||
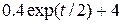
| 0.4 | ||||||||
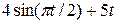
| 0.3 | ||||||||
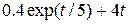
| 0.6 | ||||||||
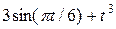
| 0.8 | ||||||||
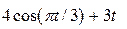
| 0.5 | ||||||||
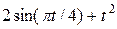
| 0.4 | ||||||||
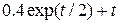
| 0.3 |
 2015-05-06
2015-05-06 1414
1414