Формула Пуазейля

Рассмотрим стационарное (ламинарное) течение несжимаемой жидкости, силами вязкого трения в которой нельзя пренебречь.

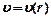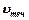Экспериментально: 1) , у стенок трубы равна нулю и максимальна на оси

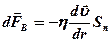2) трубы

(8) где 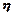- коэффициент вязкости (коэффициент внутреннего трения) 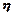~ от природы жидкости и ее температуры.

Рассмотрим малую цилиндрическую трубку тока длиной dx (рис. 5).

Модуль сил вязкого трения на боковой поверхности: .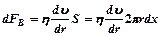

На основания этого объема

действуют силы давления, модуль результирующей которых 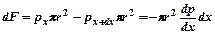(9).

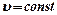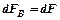При стационарном течении , то или 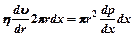. Из (8) и (9) 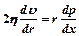(10).

Если 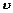на dx не изменяется 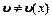, то 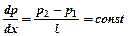(11) где р₁, р₂ – давления на входе и выходе трубки, длина которой равна l.

С учетом (11) 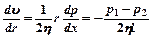(12) или 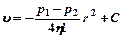,где С – постоянная

интегрирования, которую можно найти из условия,

что при r = R скорость течения равна нулю υ = 0.

Отсюда 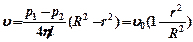(13), где 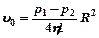(14) - скорость на оси (r =0)

Найдем объем жидкости, протекающий через сечение S за единицу времени (поток жидкости).

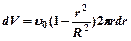- объем, протекающий за единицу времени через сечение тонкого кольца радиусом r.

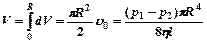(15)- формула Пуазейля ( Объем, протекающий за единицу времени через все сечение горизонтальной трубы круглого сечения )

Согласно формуле Пуазейля, поток жидкости, при ламинарном течении, пропорционален перепаду давления на единицу длины трубы и четвертой степени радиуса трубы, но обратно пропорционален коэффициенту вязкости жидкости.