О неразрывности струи: одной и той же трубки тока

(1) является выражением закона сохранения массы. Для газов (1) выполняется при скорости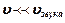

б) Уравнение Бернулли для стационарного течения идеальной жидкости (рис. 3)

Рассмотрим стационарное течение идеальной жидкости в гравитационном поле.

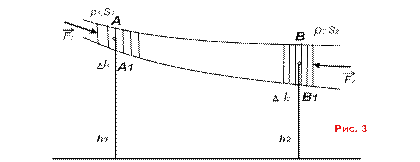Пусть за 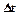объем жидкости АА₁ ВВ₁ переместится через сечение S₁ на 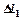, а через S₂ на расстояние .

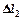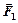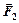Движение происходит под действием сил давления и , где , .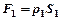

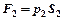При перемещении объема АА₁ ВВ₁ силы давления совершат работу:

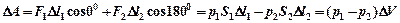(2),

где 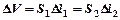^- заштрихованный объем на рисунке.

Эта работа идет на изменение энергии заштрихованного объема жидкости. При перемещении АА₁ ВВ₁ за 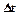изменилась 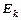и 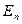только заштрихованного объема, следовательно:

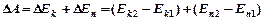
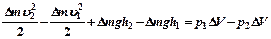
Разделим обе части этого выражение на 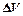и перенесем в разные стороны величины, относящиеся к сечениям S₁и S₂:

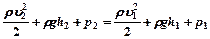(3) – уравнение Бернулли

Общий вид уравнения Бернулли: 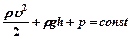(3`)

где 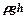- гидростатическое давление жидкости в гравитационном поле

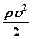- динамическое давление движущейся жидкости.

Частные случаи:

1) S₁=S₂, то и υ₁ = υ_2, тогда ;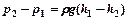

2) h₁= h₂, тогда 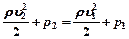, т.е. давление больше там, где скорость меньше или площадь сечения больше.

в) Формула Торричелли для скорости вытекания идеальной жидкости из отверстия (рис. 4).

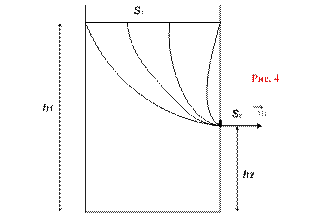
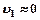, р₁ = р_атм = р₂

Применим уравнение Бернулли .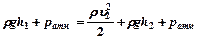

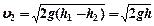(4) формула Торричелли

За dt: 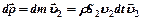(5).

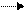Т. к. 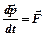, 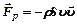(6) – сила реакции вытекающей струи = сила, действующая на сосуд.

С учетом (4) 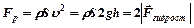(7)