С достаточной для практических расчетов точностью исследование динамических процессов в приводе механизма опрокидывания конвертера можно проводить по приведенной двухмассовой системе с одной степенью свободы (рис. 3.1). Приведение нагрузок и параметров в данном случае будем осуществлять к валу механизма поворота конвертера.
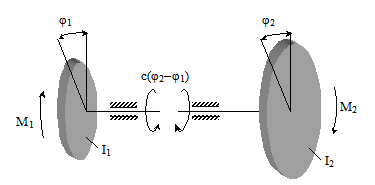
Рисунок 3.1 – Расчетная схема механизма опрокидывания конвертера
Уравнения движения системы имеют вид:
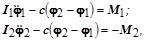 (3.13.1)
(3.13.1)
где 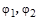 – углы поворота масс
– углы поворота масс 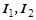 ,
, 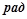 ;
;
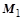 – момент электродвигателя,
– момент электродвигателя, 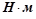 ;
;
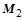 – момент опрокидывания конвертера,
– момент опрокидывания конвертера, 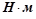 ;
;
c – коэффициент жесткости, 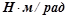 .
.
Момент опрокидывания конвертера 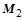 определится как функция от угла поворота корпуса конвертера
определится как функция от угла поворота корпуса конвертера 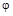 (рис. 3.2):
(рис. 3.2):
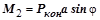 , (3.23.2)
, (3.23.2)
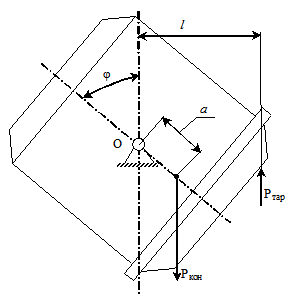
Рисунок 3.2 – Расчетная схема к определению приведенного момента опрокидывания конвертера 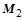 и тарировочного момента
и тарировочного момента 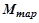
где 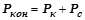 – вес корпуса конвертера и садки (определяется расчетом),
– вес корпуса конвертера и садки (определяется расчетом), 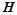 ;
;
a – расстояние от оси поворота до центра тяжести корпуса конвертера и садки (определяется расчетом);
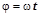 – угол наклона корпуса конвертера от вертикальной оси,
– угол наклона корпуса конвертера от вертикальной оси, 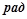 ;
;
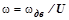 – угловая скорость поворота корпуса конвертера,
– угловая скорость поворота корпуса конвертера, 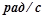 ;
;
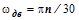 – угловая скорость вращения электродвигателя,
– угловая скорость вращения электродвигателя, 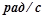 ;
;
n – частота вращения ротора электродвигателя (n =960 об/мин);
U – передаточное отношение редуктора (U =300).
Момент 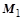 создается электродвигателем механизма опрокидывания конвертера:
создается электродвигателем механизма опрокидывания конвертера:
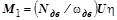 , (3.33.3)
, (3.33.3)
где 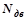 – мощность электродвигателя (
– мощность электродвигателя (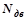 =2,5 кВт);
=2,5 кВт);
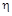 – к.п.д. передач (
– к.п.д. передач (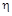 =0,6).
=0,6).
Совместное решение системы уравнений (3.1)и (3.3) с учетом зависимости (3.2) дает исходное дифференциальное уравнение для определения относительного угла закручивания 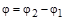 :
:
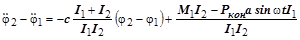
или 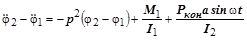 , (3.43.4)
, (3.43.4)
где 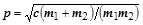 – собственная частота колебаний системы.
– собственная частота колебаний системы.
Решение дифференциального уравнения (3.4):
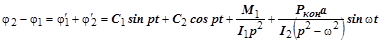 . (3.53.5)
. (3.53.5)
Постоянные интегрирования 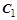 и
и 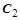 определяются из начальных условий:
определяются из начальных условий:
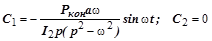 . (3.63.6)
. (3.63.6)
В результате относительный угол поворота 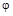 составит:
составит:
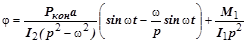 , (3.73.7)
, (3.73.7)
а величина восстанавливающего момента в упругой связи будет определяться выражением
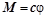 . (3.83.8)
. (3.83.8)
Коэффициент динамичности системы
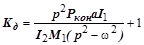 . (3.93.9)
. (3.93.9)
Рассмотренные зависимости (3.1)–(3.9) позволяют с достаточной для практических расчетов точностью приближения исследовать динамические нагрузки в вале привода механизма поворота конвертера.
Жесткость вала c можно определить по формуле (1.2).
Приведенные моменты инерции масс:
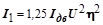 ; (3.103.10)
; (3.103.10)
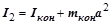 , (3.113.11)
, (3.113.11)
где 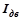 – момент инерции ротора электродвигателя (
– момент инерции ротора электродвигателя (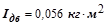 );
);
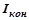 – момент инерции корпуса конвертера и садки относительно оси его поворота (определяется расчетом),
– момент инерции корпуса конвертера и садки относительно оси его поворота (определяется расчетом), 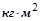 ;
;
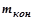 – масса корпуса конвертера и садки (определяется расчетом),
– масса корпуса конвертера и садки (определяется расчетом), 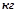 .
.
 2015-05-06
2015-05-06 294
294








