В качестве простейшей физической модели механизма может быть принята двухмассовая линейная система с одной степенью свободы. Такая схема при сравнительно простых математических выкладках дает точность первого приближения, которая удовлетворяет практическим расчетам [2].
Здесь одна концевая масса – это приведенная масса вращающихся частей механизма, вторая концевая масса – это приведенная масса поступательно движущихся частей. К массам приложены внешние нагрузки, направление и величина которых зависят от режима работы механизма. На первую массу действует приведенная ускоряющая сила при разгоне или приведенная тормозящая сила при торможении первой массы, на вторую массу действует приведенная сила статического сопротивления движению и тормозящая сила при торможении второй массы.
Вынуждающие силы считаем постоянными по величине, коэффициент жесткости также считаем постоянным.
Рассмотрим два режима неустановившейся работы механизма: подъем вверх при отсутствии зазоров в кинематических звеньях (подъем «с веса») и подъем при наличии зазоров (подъем «с подхватом»).
Подъем «с веса». При составлении уравнений движения системы используем прямой способ, мысленно отделяя массы от безмассового силового каркаса (упругого скелета), и для каждой из них записываем дифференциальные уравнения движения, заменяя действие отброшенных упругих связей их реакциями. Расчетная схема системы при подъеме «с веса» представлена на рис 2.1,а.
Дифференциальные уравнения движения системы имеют вид:
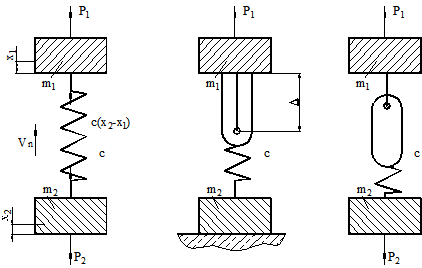
а б в
Рисунок 2.1 – Расчетная двухмассовая схема при подъеме «с веса» (а) и при подъеме «с подхватом» (б, в)
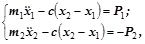 (2.12.1)
(2.12.1)
где 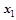 и
и 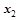 – линейные перемещения масс
– линейные перемещения масс 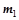 и
и 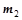 ,
, 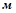 ;
;
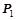 ,
, 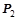 – вынуждающие силы,
– вынуждающие силы, 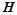 ;
;
c – коэффициент жесткости, 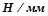 .
.
Совместное решение системы уравнений (2.12.1) с учетом ввода относительных перемещения 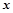 и ускорения
и ускорения 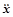 :
:
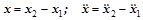 (2.22.2)
(2.22.2)
дает исходное дифференциальное уравнение для определения относительного перемещения масс 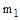 и
и 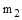 :
:
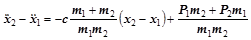 . (2.32.3)
. (2.32.3)
Общим решением уравнения (2.3)будет:
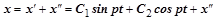 , (2.42.4)
, (2.42.4)
где 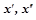 – общее и частное решения уравнения соответственно;
– общее и частное решения уравнения соответственно;
p – собственная частота колебаний, определяемая по формуле
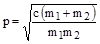 . (2.52.5)
. (2.52.5)
Постоянные 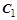 и
и 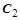 определяются из начальных условий:
определяются из начальных условий:
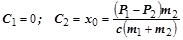 , (2.62.6)
, (2.62.6)
а частное решение –
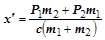 , (2.72.7)
, (2.72.7)
так что
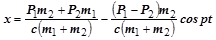 . (2.82.8)
. (2.82.8)
Из-за того, что при разгоне всегда выполняется неравенство 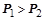 , относительное перемещение достигнет максимального значения в момент, когда
, относительное перемещение достигнет максимального значения в момент, когда 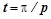 и
и 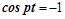 :
:
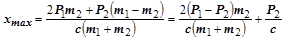 ,
,
а максимальная восстанавливающая сила
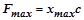 . (2.92.9)
. (2.92.9)
Подъем „с подхватом”. При подъеме «с подхватом» следует различать три этапа движения масс: 1) масса 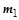 , двигаясь с начальной скоростью
, двигаясь с начальной скоростью 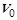 , выбирает зазор
, выбирает зазор 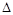 в упругом звене, включающий в себя приведенный зазор и слабину канатов (рис. 2.1,б); 2) второй этап охватывает период от начала подхвата груза к моменту возникновения в упругом звене силы, равной силе веса груза (рис. 2.1,в); 3) третий этап характеризуется общим движением обеих масс, поэтому он аналогичен движению системы при подъеме «с веса» (см. рис. 2.1,а).
в упругом звене, включающий в себя приведенный зазор и слабину канатов (рис. 2.1,б); 2) второй этап охватывает период от начала подхвата груза к моменту возникновения в упругом звене силы, равной силе веса груза (рис. 2.1,в); 3) третий этап характеризуется общим движением обеих масс, поэтому он аналогичен движению системы при подъеме «с веса» (см. рис. 2.1,а).
Максимальная сила в упругой связи возникает сразу после удара в системе, то есть в начале третьего этапа движения [2]:
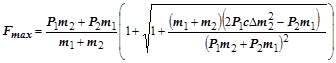 . (2.102.10)
. (2.102.10)
Формула (2.10)дает возможность определить максимальную силу в упругой связи механизма при внезапном отрыве груза от опоры.
Если масса вращающихся частей механизма велика по сравнению с массой поступательно движущихся частей (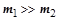 ), то допустимо использовать известную формулу
), то допустимо использовать известную формулу
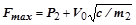 , (2.112.11)
, (2.112.11)
где 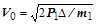 – скорость к концу выборки зазора,
– скорость к концу выборки зазора, 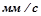 .
.
Эта формула получается из формулы (2.10), если принять 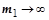 .
.
Коэффициент динамичности для обоих случаев определяется:
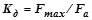 , (2.122.12)
, (2.122.12)
где 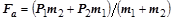 – амплитуда колебаний упругих сил,
– амплитуда колебаний упругих сил, 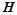 .
.
Частота и период колебаний составляют соответственно:
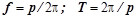 . (2.132.13)
. (2.132.13)
Таким образом, зависимости (2.1)–(2.13) разрешают определить динамические нагрузки и частотные характеристики в механизме подъема груза при подъеме «с веса» и при подъеме «с подхватом».
Движущая сила P будет создаваться электродвигателем механизма подъема груза:
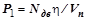 , (2.142.14)
, (2.142.14)
где 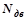 – мощность электродвигателя (
– мощность электродвигателя (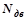 =3 кВт);
=3 кВт);
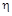 – к.п.д. передач;
– к.п.д. передач;
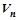 – скорость подъема груза (
– скорость подъема груза (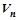 =8 м/мин).
=8 м/мин).
Сила сопротивления перемещению 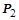 определится как сумма веса груза
определится как сумма веса груза 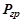 и веса подвески
и веса подвески 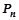 :
:
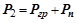 . (2.152.15)
. (2.152.15)
Масса 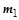 является результатом приведения массы вращающихся частей механизма к грузу (к направлению его вертикального перемещения):
является результатом приведения массы вращающихся частей механизма к грузу (к направлению его вертикального перемещения):
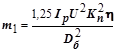 , (2.162.16)
, (2.162.16)
где 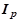 – момент инерции ротора электродвигателя (
– момент инерции ротора электродвигателя (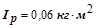 );
);
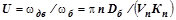 – передаточное отношение редуктора механизма подъема;
– передаточное отношение редуктора механизма подъема;
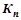 – кратность полиспаста;
– кратность полиспаста;
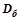 – диаметр барабана (
– диаметр барабана (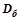 =250 мм);
=250 мм);
n – частота вращения ротора электродвигателя (n =750 об/мин).
Приведенная масса 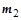 определится как сумма массы груза
определится как сумма массы груза 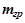 и массы подвески
и массы подвески 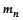 :
:
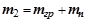 . (2.172.17)
. (2.172.17)
Для груза, подвешенного к подвижным блокам одинарного полиспаста кратностью 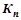 , суммарную жесткость канатов на участке от барабана к подвеске можно определить:
, суммарную жесткость канатов на участке от барабана к подвеске можно определить:
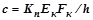 , (2.182.18)
, (2.182.18)
где 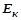 – модуль упругости каната (для канатов с органическим сердечником –
– модуль упругости каната (для канатов с органическим сердечником – 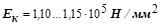 , для канатов с металлическим сердечником
, для канатов с металлическим сердечником 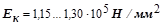 );
);
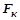 – металлическая площадь поперечного сечения каната,
– металлическая площадь поперечного сечения каната, 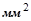 ;
;
h – вертикальная проекция расстояния от оси блока к месту закрепления каната (рис. 2.2),  .
.
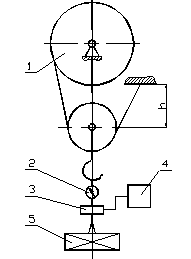
Рисунок 2.2 – Схема лабораторной установки
 2015-05-06
2015-05-06 342
342








