Операторный метод

Методика расчёта заключается в следующем.

1. Расчёт схемы до коммутации с целью вычисления независимых начальных условий.

2. Замена в обозначениях напряжений, токов, ЭДС и элементов R, L,C их изображениями в после коммутационной схеме с введением внутренних ЭДС в случае ненулевых начальных условий. Направление u_C(0)/p выбирается против тока, а Li(0) – по току.

3. Расчёт полученной схемы любым из известных методов: метод уравнений Кирхгофа, метод контурных токов и т.д., с целью получения изображений искомых величин.

4. Переход от изображений функций искомых величин к их оригиналам. Изображение искомой функции представляется в виде дроби

F(p) = 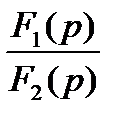, по которой находится оригинал:

1) f(t) = 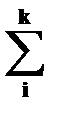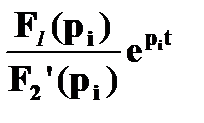, если корни знаменателя F₂ (p) p_i разные действительные, F₂^!(p) – производная знаменателя, к – количество корней.

2) f(t) = 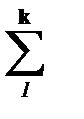2Reí 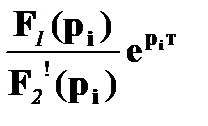ý, если корни р_i комплексно-сопряженные, к – количество комплексно-сопряженных корней.

3) f(t) =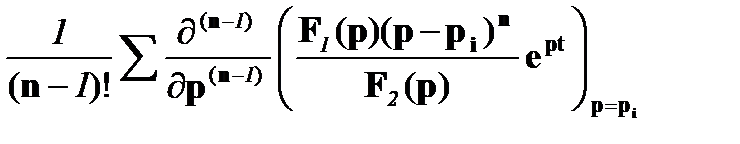

корни р_i – кратные, n - кратность корней.

Пример 2 (сх.прим.1).

i1(p) E2/p

R1 1/pC i2(p)

uc(0)/p L*i3(0)

I₂₂(p) I₁₁(p) i3(p)

E1/p R2 pL

1. Расчёт схемы до коммутации. (такой же как в прим.1)

2. Рассчитаем схему после коммутации методом контурных токов.

I₁₁(p) (R₁+pL) + I₂₂(p) R₁ = ,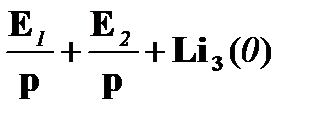

I₁₁(p) R₁ + I₂₂(p) (R₁ + R₂ + ;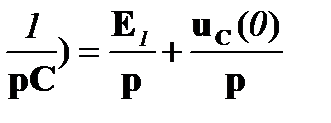

I₁₁(p) (10+0,01p) + I₂₂(p) 10 = ,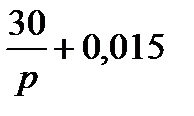

I₁₁(p) 10 + I₂₂(p) (20 + ;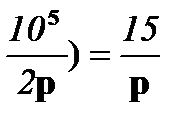

(10 + 0,01p) 10

D = = (10 + 0,01p) (20 + 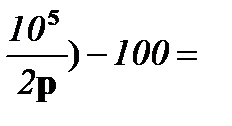600+0,2p+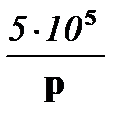

10 (20 +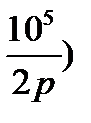

D₁ = (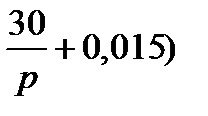 10 = (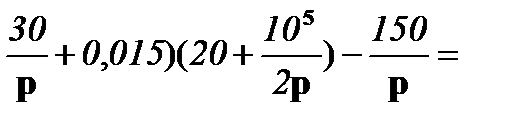

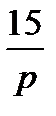(20+ ) = ;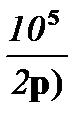

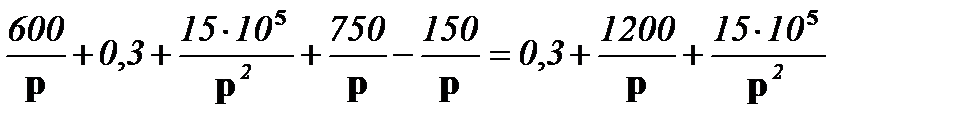10+0,01p 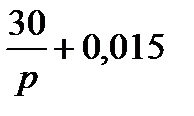=(10+0,01р) 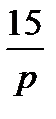-10 ( =- ;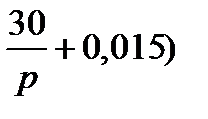

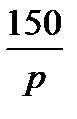D₂ = 10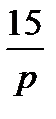

I₁₁(р) = = ;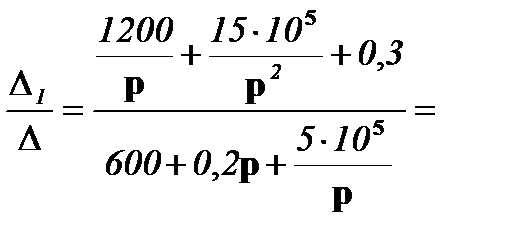

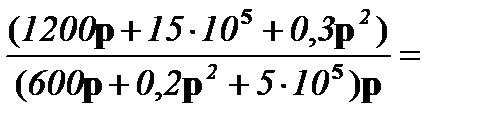
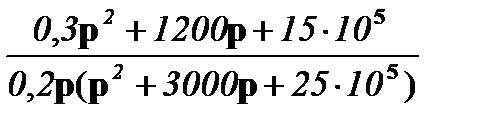I₂₂(р) = ;

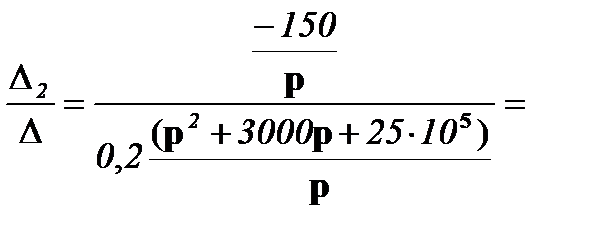
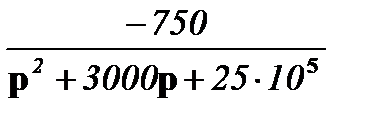I₂(р) = -I₂₂(р).

Определим i₂(t).

I₂(p) = ;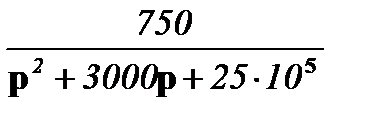

p_1,2 = -1500 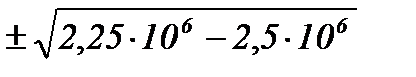= -1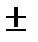500 j500;

F₁(p₁) = 750, F₂^! (p) = 2p+3000,

F₂^! (p₁) = 2 (-1500+j500) +3000 = 1000j;

I₂(t) = 2Re 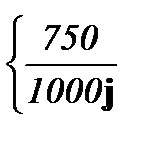e ^{(–1500+j500) t} } = 2Re{0,75e^{-j 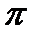/2}e^-1500t e^j500t}=

=1,5e^-1500tcos(500t- 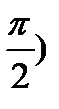=1,5e^{-1500 t}sin(500t- 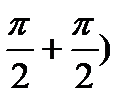= 1,5e^{-1500 t}sin 500t (A).

Проверим начальное и установившееся значения тока по его изображениям.

i_{2 уст} (¥) = lim I₂(p)*p = lim 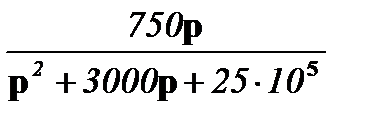= 0;

p p

i₂(0) = limI₂(p)*p = lim ;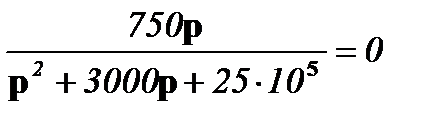

p® p®

Определим u_C(p), которое состоит из двух слагаемых: первое учитывает начальное напряжение на конденсаторе, а второе – переходное.

u_C(p)= .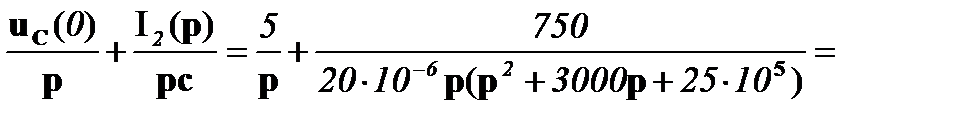

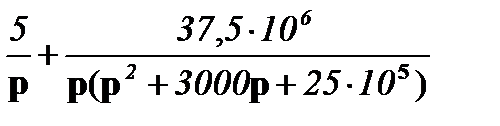В случае, когда один из корней знаменателя F₂(p) второго слагаемого равен нулю, оригинал второго слагаемого находится по формуле:

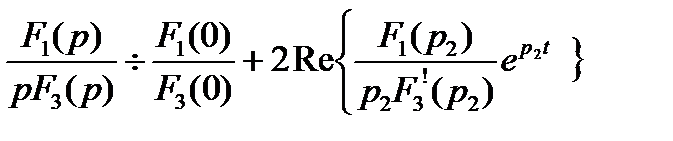, где F₃ (p) = p² +3000p + 25*10⁵,

F₃^!(p) = 2p + 3000.

Корни F₃(p): p_2,3 = -1500 .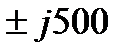

u_C(t) = 5 + =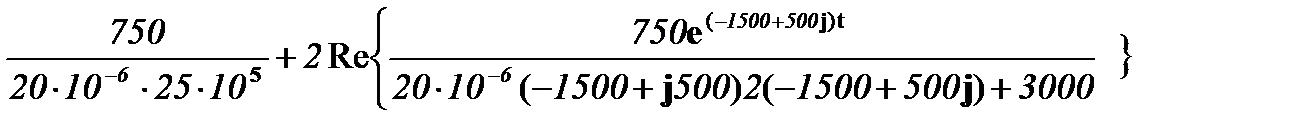

=20+750e^-1500tRe 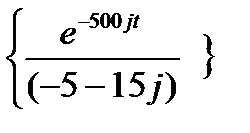= 20+750e^-1500tRe =

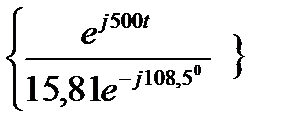=20+47,43e^-1500tcos(500t+108,5⁰)=20+47,43e^-1500tsin(500t+108,5⁰) =

=20 – 47,43e^-1500tsin(500t + 18,5⁰).

Ток i₂ и напряжение U_C, полученное двумя методами совпадают.

Исходные данные

1.Номер схемы N соответствует номеру по журналу подгруппы.

2.Rn = knN Oм, где n – номер сопротивления по схеме;

k – номер подгруппы (k = 1-4).

3. E = kN B.

4. L = 2kN мГн.

5. C = 3kN мкф.

Задание

1. Определить переходные токи во всех ветвях схемы.

2. Определить напряжение на конденсаторе.

3. Построить график напряжения на конденсаторе.

Задачу решить двумя методами: классическим и операторным.