Критерий устойчивости Михайлова

Критерий базируется на поведении кривой, которую описывает конец вектора х.у. замкнутой системы при изменении частоты от - 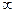до + .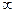

Возьмём характеристический полином следующего вида:

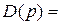
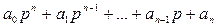(1)

Подставим в него 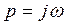и выделим вещественную и мнимую части.

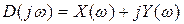
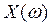- вещественная часть,

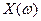
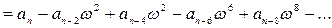
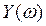- мнимая часть.

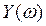
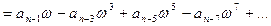
Если степень полинома нечётная(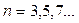), то 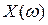имеет нечётные коэффициенты х.у., начиная с 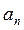и чётные степени частоты 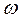. Если степень полинома чётная, то 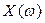имеет чётные коэффициенты х.у., начиная с 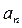, и четные степени .

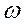Для 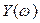степени 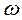будут всегда нечётными, а коэффициенты при 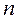- чётном –нечётные, 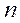-нечётном – чётные.

Изобразим годограф Михайлова выражения 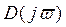на комплексной плоскости.

При ,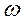

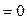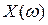
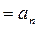
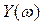
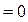
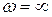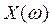
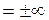
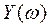
При , , 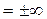знаки бесконечности зависят от показателя степени х.у.:

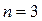
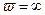
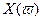
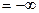
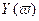
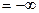
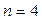
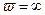
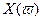
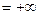
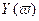
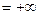
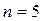
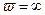
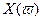
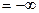
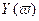
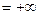
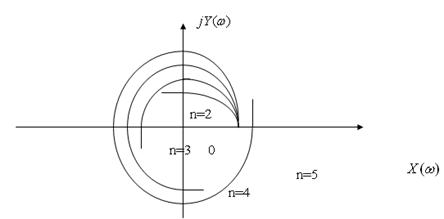
Берём значения 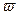и строим годограф. Для различных 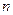годограф имеет формы, представленные на рисунке. Эти годографы называются кривыми Михайлова. Кривая Михайлова строится по точкам, рассчитывается 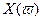и 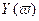для данной частоты, на кривой указываются значения частоты.

Формулировка критерия Михайлова.

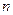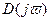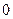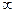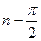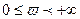Для устойчивости линейной САУ -ого порядка необходимо и достаточно, чтобы изменение аргумента функции при изменении частоты от до равнялось бы , при (4)

Другими словами, требуется, чтобы кривая Михайлова проходила последовательно 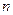квадрантов против часовой стрелки, всё время огибая начало коордиант и уходила в 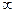в том квадранте, номер которого соответствует показателю степени полинома. Если это условие не выполняется, то система является неустойчивой.

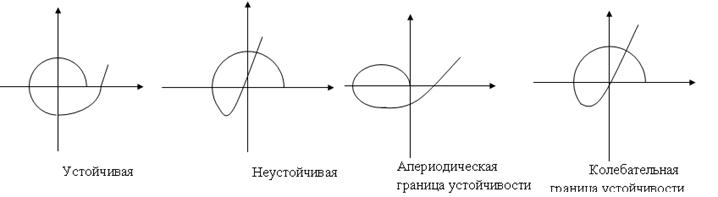
Условием нахождения системы на колебательной границе устойчивости таковы:

если 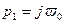- корень уравнения 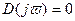, то

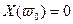
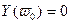
Графически это означает прохождение кривой Михайлова через начало координат. Физический смысл частоты 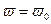в том, что она показывает частоту собственных колебаний система, когда она находится на колебательной границе устойчивости.

Важно, что очертания кривой Михайлова на границе устойчивости должны быть такими, чтобы малой деформацией кривой Михайлова в начале координат можно было удовлетворить требования устойчивости критерия Михайлова.

В формулировке критерия Михайлова показывается, что если х.у. 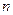-ого порядка будет иметь 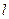корней с положительной вещественной частью, то каковы бы ни были эти корни(вещественные или комплексные), им будет соотвестсвовать суммарный угол поворота вектора 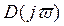, равный .

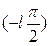Всем же остальным 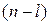корням, имеющим отрицательную вещественную часть, сумма углов поворота равна 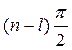. Тогда результирующий угол поворота вектора 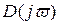при 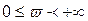будет равен:

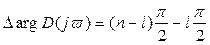(6)

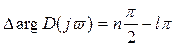(7)

Из уравнения (7), устанавливающим связь между видом кривой Михайлова и знаками вещественных частей корней х.у., вытекает формулировка критерия Михайлова при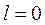

Другая формулировка критерия Михайлова:

Она состоит в использовании свойства перемежаемости корней многочленов 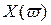и .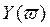

Идя по кривой Михайлова от т. 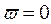в направлении возрастания частоты, мы выходим из оси 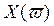, затем пересекаем ось 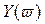, потом снова 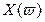и т. д.

Это значит, что корни уравнени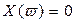й и 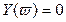(8) должны следовать поочерёдно друг за другом.

Кривые 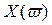и 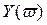имеют приблизительно такой вид:

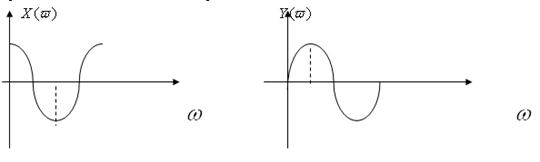
Перемежаться должны корни 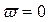, , 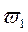,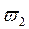… Между ними должно быть следующее соотношение: 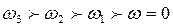(9)

Формулировка:

Условием устойчивости системы является перемежаемость корней уравнений (8). Нарушение этого условия говорит о неустойчивости системы.