2015-04-20
2060
Почти все вещества подчиняются зависимости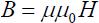 
могут быть разбиты на два класса:
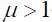– парамагнетики, в которых намагниченность вещества
увеличивает суммарное магнитное поле;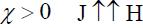 
, они
втягиваются в область сильного неоднородного магнитного поля.
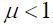– диамагнетики, в которых намагниченность уменьшает
суммарное поле; диамагнетики выталкиваются из области
сильного неоднородного поля.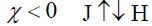 
В результате можно получить взаимосвязь векторов В и Н.
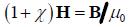
μ – магнитная восприимчивость среды: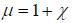 
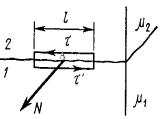
Найдем соотношение между магнитной
индукцией B и напряженностью H магнитного
поля в некоторой точке А на границе двух сред.
Проведем в точке А единичные векторы: 
– по
касательной вдоль границы раздела сред и n –
по нормали к границе, направленной от первой
среды ко второй.
Построим вблизи точки А небольшой замкнутый прямоугольный контур L,
две стороны которого параллельны вектору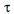 
и равны 
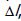, а две - вектору n
и равны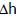 
. Предположим, что по границе раздела внутри контура вблизи
точки А не текут макротоки. Из теоремы о циркуляции вектора
напряженности магнитного поля следует, что
Это равенство должно выполняться при любом значении 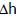и тогда в
пределе при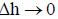 
получаем
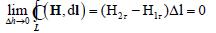
Здесь H1 и H2 - проекции напряженности H на направление
касательного орта в точке А. Поскольку последнее равенство в должно
выполняться при произвольном 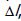, находим
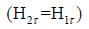
Таким образом, касательная к поверхности раздела двух сред
составляющая напряженности магнитного поля не изменяется при
переходе из одной среды в другую.
Второе условие получим с помощью теоремы Гаусса для магнитной
индукции B. Возьмем охватывающую окрестность точки А небольшую
цилиндрическую поверхность S, основания 
S которой параллельны
границе раздела и лежат по разные стороны от нее, а образующая
параллельна вектору нормали n. По теореме Остроградского-Гаусса
имеем для потока В через всю поверхность S
Это равенство должно выполняться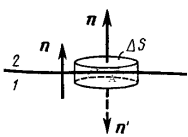 
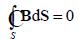
при любом значении высоты цилиндра h и в пределе получим
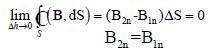
т.е. при переходе через границу раздела двух сред,
нормальная составляющая вектора магнитной индукции
не изменяется.
