Зоны Френеля

Френель предложил оригинальный метод разбиения волновой поверхности S на зоны, позволивший сильно упростить решение задач (метод зон Френеля).

Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии 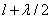от точки M (рис. 9.2). Точки сферы S, находящиеся на расстояниях 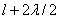, , 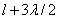и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.

Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M.

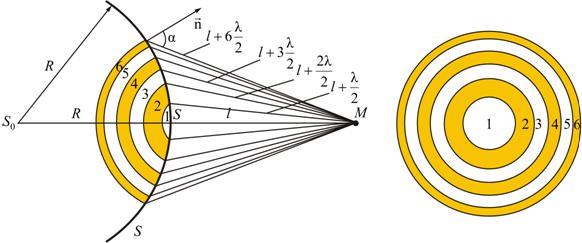
Рис. 9.2

Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга: 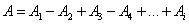, где A – амплитуда результирующего колебания, – амплитуда колебаний, возбуждаемая i-й зоной Френеля.

Величина 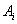зависит от площади 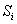зоны и угла 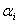между нормалью к поверхности и прямой, направленной в точку M.

Площадь одной зоны .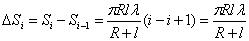

Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы.

В то же время с увеличением номера зоны возрастает угол 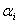и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда 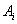. Она уменьшается также из-за увеличения расстояния до точки M: .

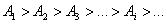Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны.

Световая волна распространяется прямолинейно. Фазы колебаний, возбуждаемые соседними зонами, отличаются на π. Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания 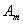от некоторой m-й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е. .

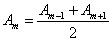Результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной 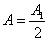, а интенсивность .