Шрёдингер сопоставил движению микрочастице комплексную функцию координаты времени, которую он назвал волновой функцией.
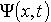 - функция, характеризующая состояние микрочастицы.
- функция, характеризующая состояние микрочастицы.
Общее временное уравнение Шредингера, позволяющее определить в любой момент времени волновую функцию 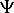 для частицы массы
для частицы массы 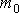 , движущейся в силовом поле
, движущейся в силовом поле 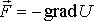 , описываемом скалярной потенциальной функцией
, описываемом скалярной потенциальной функцией 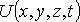 , имеет вид
, имеет вид 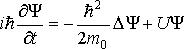 Здесь
Здесь 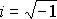 - мнимая единица, а
- мнимая единица, а 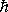 - рационализированная постоянная Планка. Стандартным символом
- рационализированная постоянная Планка. Стандартным символом 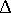 в обозначен дифференциальный оператор Лапласа, который в декартовой системе координат имеет вид
в обозначен дифференциальный оператор Лапласа, который в декартовой системе координат имеет вид 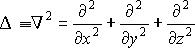 .
.
Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Частное решение для специального случая, когда 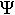 - функция не зависит от времени (стационарное состояние
- функция не зависит от времени (стационарное состояние 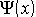 ), можно записать в виде:
), можно записать в виде: 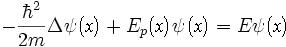 .
.
 2015-04-20
2015-04-20 545
545








