Правило Лопиталя

На основании теоремы Коши о среднем можно получить удобный метод вычисления некоторых пределов, называемый правилом Лопиталя (1661–1704).

Теорема. Пусть функци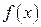и и 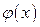непрерывны и дифференцируемы во всех точках полуинтервала 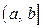и при 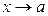совместно стремятся к нулю или бесконечности. Тогда, если отношение их производных имеет предел при 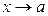, то этот же предел имеет отношение и самих функций, то есть .

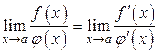Проведем доказательство данной теоремы только для случая, когда 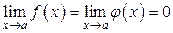. Так как пределы у обеих функций одинаковы, то доопределим их на отрезке 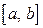, положив, что при 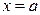выполняется равенство .

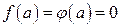Возьмем точку 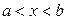. Так как функци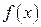и и 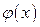удовлетворяют теореме Коши (п. 2.14), применим ее на отрезке :

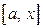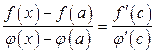, где .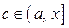

Так как 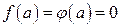, то

.

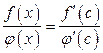Перейдем в данном равенстве к пределу:

.

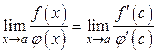Но если 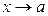, то и 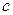, находящееся между точкам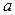и и 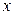, будет стремится к 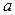, значит

.

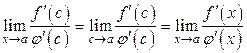Отсюда, если 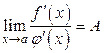, то и 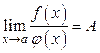, то есть

,

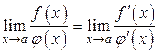что и требовалось доказать.

Если при 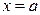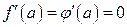, то снова получается неопределенность вида и правило Лопиталя можно применять снова, то есть

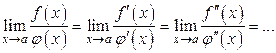
Доказательство правила Лопиталя для случая проводится сложнее, и мы его рассматривать не будем.

При раскрытии неопределенностей типа 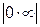, , 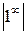, , 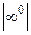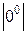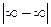правило Лопиталя применять непосредственно нельзя. Вначале все эти неопределенности необходимо преобразовать к виду или .

Правило Лопиталя может быть использовано при сравнении роста функций, в случае когда 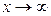. Наибольший практический интерес здесь представляют функции 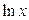, , 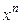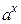. Для этого найдем пределы их отношений:

1) 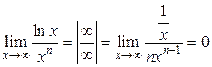, значит, растет быстрее, чем ;

2) 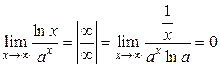, значит, 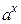растет быстрее, чем ;

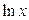3) 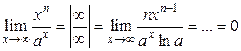, значит, 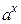растет быстрее, чем .

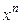Отсюда следует, что быстрее всего растет 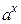, затем 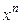и, наконец, .

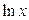Экстре́мум (лат. extremum — крайний) в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум).

Содержание [убрать] · 1 Определения · 2 Замечание · 3 Необходимые условия существования локальных экстремумов · 4 Достаточные условия существования локальных экстремумов · 5 См. также

[править]Определения

Пусть дана функция 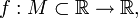и 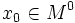— внутренняя точка области определения 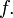Тогда

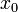· называется точкой локального максимума функции 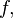если существует проколотая окрестность 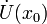такая, что

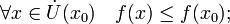
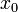· называется точкой локального минимума функции 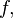если существует проколотая окрестность 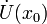такая, что

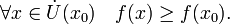
Если неравенства выше строгие, то 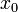называется точкой строгого локального максимума или минимума соответственно.

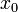· называется точкой абсолютного (глобального) максимума, если

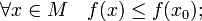
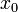· называется точкой абсолютного минимума, если

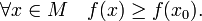
Значение функции 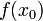называют (строгим) (локальным) максимумом или минимумом в зависимости от ситуации. Точки, являющиеся точками (локального) максимума или минимума, называются точками (локального) экстремума.

[править]Замечание

Функция 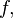определённая на множестве 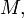может не иметь на нём ни одного локального или абсолютного экстремума. Например,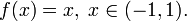

[править]Необходимые условия существования локальных экстремумов

· Из леммы Ферма вытекает следующее:

Пусть точка 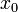является точкой экстремума функции 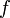, определенной в некоторой окрестности точки .

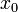Тогда либо производная 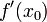не существует, либо .

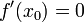(Математический Анализ. Том 1. Л. Д. Кудрявцев. Москва «Высшая Школа» 1973 г.)

[править]Достаточные условия существования локальных экстремумов

· Пусть функция 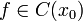непрерывна в 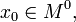и существуют конечные или бесконечные односторонние производные 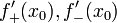. Тогда при условии

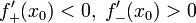
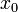является точкой строгого локального максимума. А если

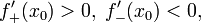
то 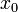является точкой строгого локального минимума.

Заметим, что при этом функция не дифференцируема в точке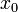

· Пусть функция 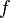непрерывна и дважды дифференцируема в точке 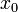. Тогда при услови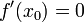и

и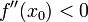

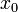является точкой локального максимума. А есл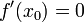и

и

то 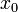является точкой локального минимума.

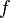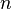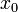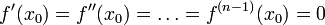· Пусть функция дифференцируема раз в точке и , а .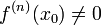

Если 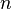чётно и 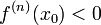, то 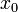- точка локального максимума. Если 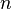чётно и 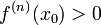, то 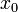- точка локального минимума. Если 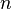нечётно, то экстремума нет.