2015-04-20
662
Косвенные измерения − это измерения, при которых искомое значение A находят на основании известной функции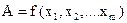 
, где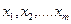 
− значения, полученные при прямых измерениях. Их обработка и представление результатов проводятся в зависимости от наличия или отсутствия связи (корреляции) при проведении этих измерений. Подход к решению задачи нахождения результата косвенных измерений заключается в разложении функции f (достаточно гладкой) в ряд Тейлора в окрестности 
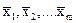[1-3] и учете только членов первого порядка малости.
Оценка результата косвенного измерения: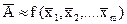 
, где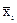 
− оценка результата i − го аргумента. Оценка СКО случайной погрешности S(
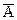) результата косвенного измерения вычисляется по формуле: S( ) ≈ 
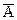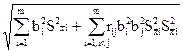, где -1 < 
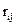< 1 − оценка коэффициента корреляции между погрешностями аргументов 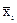и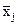 
; 
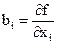− так называемые коэффициенты влияния i − го аргумента. Корреляция между аргументами чаще всего возникает тогда, когда их измерения проводятся одновременно и подвергаются одинаковому влиянию внешних условий: температуры, влажности, помех и т.д. Точное определение 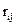обычно затруднено [1-3]. Часто рассматриваются случаи, когда имеется полная статистическая связь 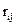= 1 и ее полное отсутствие 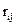= 0.
При отсутствии корреляционной связи между аргументами СКО результата косвенного измерения S( 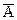), обусловленного случайными погрешностями, вычисляется по формуле: S( ) = 
,
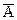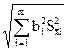где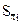 
− среднее квадратическое отклонение результата измерения аргумента 
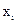, рассчитанное по формуле 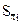= S 
/ 
= 
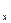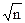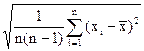, а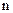 
− число измерений i− го аргумента.
Для случая косвенного измерения при линейной зависимости между аргументами: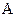 
= 
, 
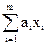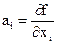где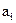 
− постоянный коэффициент i− го аргумента, m − число аргументов.S( ) = 
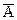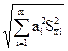, Если 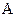= k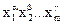 
, и k, 
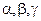− константы, то определив частные производные по 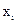, подставив их в формулу для S( 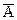) и разделив полученное выражение на 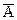, получим: 
= 
= 
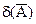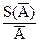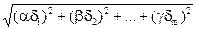. Здесь 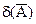и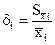 
− относительные среднеквадратичные отклонения случайных погрешностей результата измерения 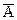и i− го аргумента Обычно считается, что случайные величины распределены по нормальному закону. При большом числе измерений (более 25-30) выполненных при нахождении каждого аргумента, доверительную границу случайной погрешности результата косвенного измерения определяют по формуле e(P) = zp S( 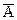), здесь zp – квантиль нормального распределения, соответствующий выбранной доверительной вероятности Р. При меньшем числе измерений используется распределение Стьюдента, число степеней свободы которого рассчитывается по приближенной формуле: k =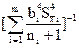 
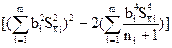, где ni - число измерений при определении аргумента 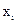. В этом случае доверительная граница случайной погрешности результата косвенного измерения e(P) = tpS( 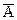), где tp - коэффициент Стьюдента, соответствующий доверительной вероятности Р = 1-q и числу степеней свободы k. Систематическая погрешность результата косвенного измерения определяется систематическими погрешностями результатов измерений аргументов. При измерениях их стараются исключить. До конца это сделать не удается; всегда остаются неисключенные систематические погрешности, которые рассматриваются как реализации случайной величины, имеющей равномерное распределение. Доверительные границы неисключенной систематической погрешности результата косвенного измерения q(Р), в случае, когда неисключенные систематические погрешности аргументов заданы границами qi равны:q(Р) = k 
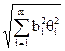где k - поправочный множитель, определяемый принятой доверительной вероятностью Р и числом m составляющих qi.Его значения приведены в таблице.
Результат косвенного измерения записывается в виде х ± D(Р) при доверительной вероятности Р.
