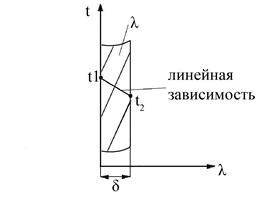
При известных температурах t1 и t2, λ, толщине d и теплопроводности λ, требуется найти распределение температур внутри стенки, а также количество тепла, проходящее через нее. Рассмотрим стационарный случай.
Условия стационарности: 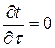
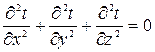 – уравнение Лапласа
– уравнение Лапласа
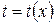
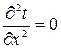
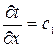 (I – интегрирование);
(I – интегрирование);
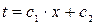 (II – интегрирование) – общее решение.
(II – интегрирование) – общее решение.
Используя граничные условия I ряда, получим:
1. 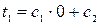 Þ
Þ 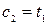
2. 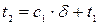 Þ
Þ 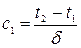 Þ
Þ 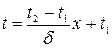
Формула (12.7) по линейному закону описывает распределение температур по толщине стенки.
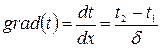 Þ
Þ 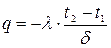 Þ
Þ 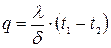 (12.8)
(12.8)
Формула (12.8) определяет количество тепла, проходящего через стенку.
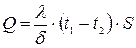 (12.9)
(12.9)
где S – площадь стенки
Формула (12.9) - выражает полное количество тепла, проходящего через стенку площади S.
Из формулы (12.8) 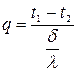
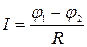
Исходя из аналогии закона Фурье и закона Ома величину называют термическим сопротивлением плоской стенки.
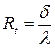 (12.10)
(12.10)
 2015-04-23
2015-04-23 292
292








