2015-04-23
3553
Розглядаючи формули алгебри логіки (табл. 2.1) та приклад таблиці істинності (табл. 2.2), неважко бачити, що ліві та праві частини тотожностей по суті являють собою функції логічних змінних, якими є прості висловлення, причому ці функції приймають значення 0 або 1 у функціональній залежності від набору значень істинності аргументів. В подальшому значення істинності логічних змінних і функцій цих змінних будемо називати просто їх значеннями. Тому можемо увести наступне формалізоване означення логічної функції.
Означення 2.2. Функція f (x 1, x 2,..., xn) называється логічною (перемикальною, булевою), якщо вона, так само як її аргументи (логічні змінні) xi, i =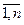 
, може приймати тільки два значення: 0 та 1.
Означення 2.3. Упорядкована множина значень аргументів логічної функції називається набором і позначається кортежем (а 1, а 2,..., аі,..., аn), аі Î{0, 1}, i = .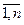
Областю визначення логічної функції (ЛФ) n змінних є сукупність всіх можливих упорядкованих наборів. Набір уявляє собою число у двійковій системі числення, якому відповідає певне число в десятковій системі числення (Додаток А). Ці числа можна розглядати як номер набору у відповідній системі числення. У такий спосіб встановлюється порядкова нумерація наборів для будь-якої ЛФ, як це показано в таблиці 2.2. Таким чином, будь-яким набором (а 1, а 2,..., аі,..., аn) задається його власний порядковий номер у двійковій та десятковій системах числення і в той же час в його i -му розряді (i = 1, 2, …, n) знаходиться значення 0 або 1 змінної xi даного набору.
|
|
|
Приймаючи до уваги поняття набору, логічній функції можна дати також наступне означення.
Означення 2.4. логічною функцією (функцією алгебри логіки) називається функція f (x 1, x 2,. .., xn), яка приймає значення 0 або 1 на наборах логічних змінних x 1, x 2,. .., xn.
Оскільки кожний з n аргументів логічної функції може приймати два можливих значення, то очевидно, що областю визначення логічної функції n змінних є сукупність m =2 n можливих наборів.
Оскільки логічна функція n аргументів може приймати тільки два з можливих значень (0 і 1) на кожному з m наборів, то кількість всіх різних логічних функцій n аргументів дорівнює k =2 m. Значення величин m і k обчислюються за формулами комбінаторики (Додаток Б).
Означення 2.5. Якщо логічна функція n змінних визначена на всіх 2 n наборах, її називають повністю визначеною, в протилежному випадку – неповністю визначеною.
Для наборів, на яких ЛФ не визначена, її значення можна прийняти будь-яким із множини {0, 1} і таким чином привести її до повністю визначеної.
Логічну функцію можна задати її вербальним описом. Наприклад: “Функція трьох аргументів приймає значення 1, якщо два аргумента або всі три дорівнюють 1, а в інших випадках вона приймає значення 0”.
|
|
|
Для задання логічної функції можна застосувати табличний спосіб, коли функція представляється своєю таблицєю істинності. Прикладом може служити таблиця 2.2 істинності функції F =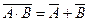 
. При більшій ніж 2 кількості аргументів табличний спосіб незручний через великий розмір таблиці. Логічна функція може бути задана також у вигляді формули, наприклад: f (x 1, x 2, x 3)= x 1Ú 
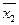Ú x 3.
Логічні функції одного і двох аргументів називають елементарними. Їх можна задати як формулами, так і таблицями істинності.
Для логічної функції одного аргумента існують два набори, кількість таких функцій – чотири, згідно переліку:
f (x)=0, має назву “Константа нуль”;
f (x)= x, має назву “Змінна x ” (повторення x);
f (x)=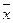 
, має назву “Інверсія (заперечення) x ”;
f (x)=1, має назву “Константа одиниця”.
Цей перелік по суті співпадає з переліком логічних операцій над простим висловленням, наведеним у п.2.2. Опис цих функцій подано таблицєю 2.3.
Таблиця 2.3 – Таблиця істинності логічних функцій f (x)
| Номер набору | x | f (x)=0 | f (x)= x | f (x)=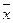
| f (x)=1 |
Для логічної функції двох аргументів існують чотири набори, кількість таких функцій – шістнадцять. Відповідність цих функцій переліку операцій алгебри логіки, наведеному в п.2.2, зручніше буде пояснити на підставі таблиці 2.4.
Таблиця 2.4 – Таблиця істинності логічних функцій f (x 1, x 2)
| № | x 1 | x2 | ||||||||||||||||
У 16 клітинках першого рядка таблиці 2.4 розміщені номери i =0, …, 15 функцій fі (x 1, x 2), а в тих же за номерами клітинках інших рядків – виділені жирним шрифтом значення функцій fі (x 1, x 2) для відповідних наборів. Неважко бачити, що немає жодної пари функцій з однаковими значеннями на всіх наборах, тобто всі функції різні. Наведемо назви цих функцій у відповідності до логічних операцій, які вони реалізують:
f 0(x 1, x 2)=0, має назву “Константа нуль”;
f1 (x 1, x 2)= x 1Ù x 2, має назву “Кон’юнкція” (функція “І”);
f 2(x 1, x 2)=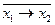 
, має назву “Заборона x 2”;
f 3(x 1, x 2)= x 1, має назву “Змінна x 1”;
f4 (x 1, x 2)=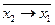 
, має назву “Заборона x 1”;
f 5(x 1, x 2)= x 2, має назву “Змінна x 2”;
f 6(x 1, x 2)= x 1Å x 2, має назву “Сума за модулем 2” (логічна нерівнозначність, виключне “або”);
f 7(x 1, x 2)= x 1Ú x 2, має назву “Диз’юнкція” (функція “Або”);
f 8(x 1, x 2)= x 1¯ x 2, має назву “Функція (стрілка) Пірса” (функція “Або-Не”);
f 9(x 1, x 2)= x 1~ x 2, має назву “Рівнозначність”;
f 10(x 1, x 2)=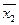 
, має назву “Інверсія x 2” (функція “Не”);
f 11(x 1, x 2)= x 2® x 1, має назву “Імплікація від x 2 до x 1” (функція “Якщо-То”);
f 12(x 1, x 2)=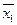 
, має назву “Інверсія x 1” (функція “Не”);
f 13(x 1, x 2)= x 1® x 2, має назву “Імплікація від x 1 до x 2” (функція “Якщо-То”);
f 14(x 1,x2)= x 1| x 2, має назву “Функція (штрих) Шеффера” (функція “І-Не”).
f 15(x 1, x 2)=1, має назву “Константа одиниця”.
З числа ЛФ двох змінних f 0 – f 15 (табл. 2.4) можна виділити базисні, за допомогою яких можна одержати будь-які інші ЛФ. У той же час базисні ЛФ неможливо одержати за допомогою інших. До базисних належать такі елементарні ЛФ: f 0, f 1, f 3, f 5, f 7, f 10, f 12, f 15.
За допомогою елементарних ЛФ можна будувати складні ЛФ від довільної скінченної кількості аргументів. Будь-яка складна ЛФ може бути поданою у вигляді формули, яка вказує послідовність елементарних логічних операцій над логічними змінними. Пріоритет виконання операцій у формулах такий: спочатку виконуються операції всередині дужок, після чого – операції заперечення, потім кон’юнкції, а далі – диз’юнкції та всі інші операції в порядку запису зліва направо.
|
|
|
Логічні вирази, тобто формули, які містять операції диз’юнкції та кон’юнкції, можна перетворювати (розкривати дужки, виносити загальний множник, переставляти місцями члени і т.п.) за правилами алгебри чисел,вважаючи формально диз’юнкцію операцією додавання, а кон’юнкцію - операцією множення. Але потрібно чітко пам’ятати, що в алгебрі логіки, на відміну від алгебри чисел, знаки додавання і множення означають логічні зв’язки “Або” та“І”.
Формулу будь-якої ЛФ можна, використовуючи операції алгебри логіки та опис елементарних функцій, перетворити до такого виду, щоб усі логічні зв’язки проміж логічними змінними визначалися операціями диз’юнкції, кон’юнкції та інверсії. Покажемо це для ЛФ двох змінних f 2, f 4, f 6, f 8, f 9, f 11, f 13, f 14 (табл. 2.4), які не є базисними:
f 2(x 1, x 2)= =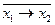 
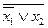= x 1Ù ;
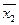f4 (x 1, x 2)= =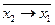 
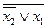= x 2Ù ;
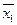f 6(x 1, x 2)= x 1Å x 2=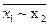 
= 
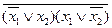=(x 1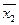Ù )Ú(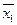 Ù x 2);
f 8(x 1, x 2)= x 1¯ x 2=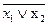 
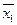= Ù ;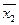
f 9(x 1, x 2)= x 1~ x 2= x 1Ù x 2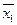Ú Ù ;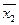
f 11(x 1, x 2)= x 2® x 1= 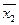Ú x 1;
f 13(x 1, x 2)= x 1® x 2= 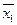Ú x 2;
f 14(x 1,x2)= x 1| x 2=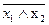 
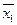= Ú .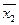
Розглянемо особливі випадки, коли мають місце такі співвідношення між аргументи ЛФ: один з двох аргументів є константою 1 або 0; обидва аргументи дорівнюють один одному (x 1= x 2= x); один з аргументів є інверсією іншого (x 1= x, x 2= 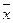). У таких випадках мають місце наступні тотожності:
x Ú1=1, x Ù1= x, x ~1= x, x Å1= ,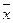
x ®1=1, 1® x = x, x |1= 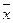, x ¯1=0;
x Ú0= x, x Ù0=0, x ~0= 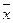, x Å0= x,
x ®0= 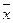, 0® x =1, x |0=1, x ¯0= ;
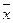x Ú x = x, x Ù x = x, x ~ x =1, x Å x =0, x ® x =1, x | x = 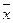, x ¯ x = ;
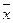x Ú 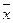=1, x Ù 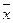=0, x ~ 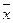=0, x Å 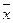=1,
x ® 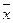= 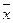, 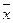® x = x, x | 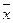=1, x ¯ 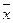=0.
Доведення правильності наведених вище перетворень формул логічних функцій легко здійснюється за допомогою таблиць істинності (аналогічно табл. 2.2), за збіжністю значень лівої та правої частин рівності, що доводиться.
Розглянути так само логічні функції трьох аргументів неможливо, оскільки їх кількість становить 28= 256. Проте це не має принципового значення, бо аргументи будь-якої ЛФ також можуть бути логічними функціями. Це означає, що створювати складні ЛФ можна шляхом підстановки інших ЛФ в якості аргументів.
|
|
|
Означення 2.6. Функція F (f 1,…, fn), що одержується із функції F (x 1,…, xn) шляхом підстановки функцій f 1(x 1,…, xn),…, fn (x 1,…, xn) замість аргументів x 1,…, xn, називається суперпозицією функцій f 1,…, fn.
Таким чином, знаючи властивості логічних функцій та принцип суперпозиції, можна з простих логічних висловлень утворювати складніші, або, що те ж саме, з простих логічних функцій одержувати складні. Слід помітити, що при виконанні операції підстановки функцій f 1,…, fn замість аргументів у формулу функції F (x 1,…, xn) не виключається можливість заміни не всіх аргументів. Крім того, серед аргументів функцій f 1,…, fn можуть бути відсутніми деякі зі змінних x 1,…, xn. тоді, після перейменування аргументів, буде одержана функція G (y 1,…, ym) з числом аргументів m < n. Саме такі випадки віддзеркалює наступний приклад.
Результати наведених вище перетворень формул ЛФ та використання суперпозиції є такими, що всі логічні зв’язки проміж логічними змінними визначаються операціями диз’юнкції, кон’юнкції та інверсії. Це означає, що відповідні цим операціям елементарні функції fІ (x 1, x 2)= x 1Ù x 2 (функція “І”), f Або(x 1, x 2)= x 1Ú x 2 (функція “Або”), f Не(x)=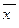 
(функція “Не”) створюють систему логічних функцій, яка володіє властивістю функціональної повноти. Наведемо формальне означення цього поняття.
Означення 2.7. 
Набір елементарних ЛФ, за допомогою якого можна подати будь-яку ЛФ, використовуючи закони алгебри логіки, суперпозиції та підстановки, називається функціонально повним.
Система всіх розглянутих вище елементарних ЛФ є функціонально повною, однак надлишковою. Меншою за складом є згадана вище система базисних фнкцій f 0, f 1, f 3, f 5, f 7, f 10, f 12, f 15 (табл. 2.4), але й ця система є надлишковою. Найменшою надлишковістю володіє згадана вище функціонально повна система “І–Або–Не”: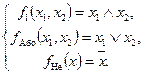 
(2.1)
Система (2.1) надлишкова, оскільки з неї можна вилучити або 
диз’юнкцію, або кон’юнкцію без втрати повноти. Вилучену функцію можна дістати з інших двох, що залишилися, відповідно до законів алгебри логіки. Наприклад, виключивши із (2.1) кон’юнкцію f І(x 1, x 2), останню одержують, застосувавши заперечення у функції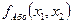 
до окремих доданків і до всього виразу в правій частині: 
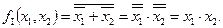
Отже, через вилучення із системи (2.1) кон’юнкції f І(x 1, x 2) набір функцій 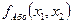та f Не(x) не втрачає функціональної повноти. Однак, якщо із набору 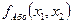та f Не(x) вилучити хоча б одну з цих функцій, то отриманий набір у складі однієї функції вже не буде функціонально повним.
Означення 2.8. Якщо з функціонально повного набору елементарних ЛФ не можна вилучити жодної функції без втрати його повноти, то такий набір називають базисом.
Базисами логічних функцій є: {Ù,` } – кон’юнктивний базис; {Ú,` } – диз’юнктивний базис; {®} – імплікативний базис, де x 1® x 2= 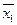Ú x 2; {¯} – базис Вебба (Пірса), де х 1¯ х 2= f 8(х 1, х 2)= 
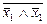= х 1Ú х 2; {|} – базис Шеффера, де х 1| х 2= f 14(х 1, х 2)=` х 1Ú` х 2= 
.
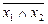Для кожної складної ЛФ можна отримати еквівалентну до неї функцію в будь-якому з перерахованих базисів. Наприклад, ` х 1Ú х 2Ù х 3= х 1®(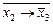
).
Помітимо, що функціонально повна система (2.1) “І–Або–Не” формально не є базисом. Проте, вона широко застосовується при аналітичному поданні й перетвореннях логічних функцій та при технічній реалізації останніх у пристроях дискретної дії (дискретних пристроях). Тому набір функцій (2.1) умовно відносять до числа базисів.
Завершуючи розгляд властивостей логічних функцій та їх перетворень, уведемо ще три специфічні поняття.
Означення 2.9. Логічна функція називається інверсною по відношенню до іншої, якщо вона одержується із останньої шляхом інверсії її значень на всіх наборах.
Кожна з функцій f 0 – f 15 має інверсну (табл. 2.4). Наприклад, f 0=Ø f 15, f 1=Ø f 8, f 2=Ø f 15.
Означення 2.10. Дві логічні функції з однаковою кількістю аргументів рівносильні одна одній, якщо вони приймають на всіх наборах однакові значення.
Означення 2.11. Логічна змінна xi є дійсною, якщо значення логічної функції f (x 1, x 2,..., xn) змінюється при зміні значення xi. В протилежному випадку ця змінна для даної функції є фіктивною, тобто не є її аргументом.
Поняття рівносильності ЛФ, дійсності та фіктивності їх аргументів необхідні для розуміння того, що в практичних застосуваннях може бути необхідним здійснити аналіз ЛФ з невизначеним числом аргументів, для якої потрібно створити аналітичний вираз, маючи на увазі, що частина аргументів, включених з надлишковістю у список аргументів ЛФ, можуть дійсно бути аргументами даної функції. Цей факт з’ясовується у підсумку проведеного аналізу ЛФ.
