Одним з видів відношень, дуже важливим в аспекті практичного застосування, є віповідність.
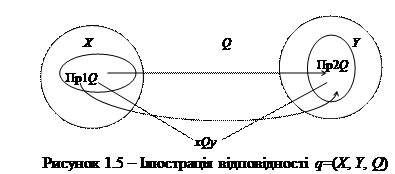
Означення 1.18. Відповідністю q називається трійка множин (X, Y, Q), в якій X - область відправлення відповідності, Y - область прибуття відповідності, Q - множина, яку називають графіком відповідності.
Серед елементів множин X і Y можуть бути такі, що не входять ні в одну із пар (x, y) відповідності Q. Тому з кожною відповідністю пов’язані ще дві множини:область визначення та область значень.
Означення 1.19. Область визначення відповідності - це елементи множини Х (позначення Пр1 Q), які беруть участь у відповідності (X, Y, Q).
Означення 1.20. О бласть значень відповідності – це елементи множини Y (позначення Пр2 Q), які беруть участь у відповідності (X, Y, Q).
Позначення Пр1 Q і Пр2 Q областей визначеннятазначень відповідності мають сенс проекцій множини Q на множини X та Y відповідно. Тому очевидно, що область визначення є підмножиною області відправлення, а область значень є підмножиною області прибуття:.Пр1 Q Í X, Пр2 Q Í Y.
Якщо (x, y)Î Q, тоді кажуть, що елемент у відповідає елементу х (позначення 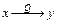 або хQy). Графічну ілюстрацію відношення відповідності наведено на рис. 1.5.
або хQy). Графічну ілюстрацію відношення відповідності наведено на рис. 1.5.
 Оскільки графіком Q відповідності q визначаються упорядковані пари (x, y), то очевидно, що останні є елементами декартова добутку множин X ´ Y, тобто Q Í(X ´ Y). Тому часто графік Q відповідності називають просто відповідністю. Прикладом відповідності є описаний вище (пп. 1.1, 1.3) декартов добуток А ´ В множин А і В, якщо відповідністю охоплені всі можливі пари (а, b):
Оскільки графіком Q відповідності q визначаються упорядковані пари (x, y), то очевидно, що останні є елементами декартова добутку множин X ´ Y, тобто Q Í(X ´ Y). Тому часто графік Q відповідності називають просто відповідністю. Прикладом відповідності є описаний вище (пп. 1.1, 1.3) декартов добуток А ´ В множин А і В, якщо відповідністю охоплені всі можливі пари (а, b):
Для задання відповідності можуть бути використані будь-які способи задання відношень: перерахуванням упорядкованих пар, пов’язаних відношенням відповідності, як у прикладах 1.24, 1.25; графіком Q відповідності (X, Y, Q) у вигляді матриці, кожен елемент aij якої дорівнює 1, якщо хiQyj, і 0 у протилежному випадку. Наприклад, графік відповідності Q ={(a, 1), (a, 2), (b, 1), (с, 2), (с, 4), (с, 9), (d, 16)} подається такою матрицею:
| (X, Y, Q) | |||||
| a | |||||
| b | |||||
| c | |||||
| d |
Задання цієї ж відповідності графом подано на рис. 1.6. Відмінність графа відповідності (рис. 1.6) від графа відношення (рис. 1.4) полягає у відсутності позначок (точками) елементів хi Î X та yj Î Y, що не беруть участі у відповідності Q.
Якщо області визначення та значеньвідповідності є підмножинами однієї множини, то говорять, що має місце відповідність на множині. Очевидно, що у такому випадку відповідність Q Í А ´ A є підмножиною (в загальному випадку нестрогою) декартова добутку А ´ A = A 2 з квадратною матрицею її графіка.
Відповідності на множинах володіють такими ж властивостями, як і бінарні відношення, тобто відповідність Q Í А 2 є: рефлексивною, якщо якщо (a, a)Î Q (або aQa) для всіх a Î А, що беруть участь у відповідності; антирефлексивною, якщо для всіх (a, b)Î Q має місце нерівність a ≠ b; симетричною, якщо для всіх пар (a, b)Î Q існують пари (b, a)Î Q; антисиметричною, якщо для всіх a Î А і b Î А із (a, b)Î Q і (b, a)Î Q слідує a = b; транзитивною, якщо для всіх a Î А, b Î А і c Î А з того що (a, b)Î Q і (b, c)Î Q слідує (а, c)Î Q, а також лінійною, якщо b = a, aQb і bQa для всіх a,b Î А.
Читачеві надається можливість самостійно виявити особливості матриць і графів, якими задаються відповідності, що володіють такими властивостями.
 Для кожної відповідності q =(X, Y, Q), Q Í X ´ Y існує обернена відповідність, яка отримується, якщо дану відповідність q розглядати в зворотному напрямку, тобто визначати елементи x Î X, з якими зіставляються елементи y Î Y. Відповідність, обернена до відповідності q, позначається так: q –1=(Y, X, Q –1), де Q –1Í Y ´ X, причому (Q– 1)–1= Q. Зрозуміло, що перехід від Q до Q –1 здійснюється взаємною перестановкою координат кожної впорядкованої пари. Слід зазначити, що при переході від Q до Q –1 область визначення стає областю значень і навпаки. Матриця графіка відповідності Q –1 – це транспонована матриця графіка Q.
Для кожної відповідності q =(X, Y, Q), Q Í X ´ Y існує обернена відповідність, яка отримується, якщо дану відповідність q розглядати в зворотному напрямку, тобто визначати елементи x Î X, з якими зіставляються елементи y Î Y. Відповідність, обернена до відповідності q, позначається так: q –1=(Y, X, Q –1), де Q –1Í Y ´ X, причому (Q– 1)–1= Q. Зрозуміло, що перехід від Q до Q –1 здійснюється взаємною перестановкою координат кожної впорядкованої пари. Слід зазначити, що при переході від Q до Q –1 область визначення стає областю значень і навпаки. Матриця графіка відповідності Q –1 – це транспонована матриця графіка Q.
Означення 1.21. Якщо матриця графіка Q прямої відповідності (X, Y, Q) співпадає зі своєю транспонованою відносно головної діагоналі матрицею, то відповідність (X, Y, Q) називається взаємно однозначною. При цьому транспонована матриця є матрицєю графіка Q –1 відповідності (Y, X, Q –1), оберненої до прямої відповідності (X, Y, Q).
Означення 1.22. Композицією відповідностей (як і будь-яких відношень) називається послідовне застосування двох відповідностей, тобто композиція p ○ q відповідностей q і p – це операція над трьома множинами X, Y, Z, на яких визначені дві відповідності: q =(X, Y, Q), Q Í X ´ Y; p =(Y, Z, P), P Í Y ´ Z, причому область значень першої відповідності (q) збігається з областю визначення другої відповідності (p): Пр2 Q = Пр1 Р.
Для опису відповідностей між множинами використовують поняття відображення однієї множину в іншу, як частковий випадок відповідності. Для задання відображення потрібно вказати: множину А, яка відображається, тобто область визначення відображення; множину В, в яку відображається область визначення, тобто область значень відображення; закон відповідності між цими множинами, за яким для елементів першої множини вибираються елементи із другої множини.
Означення 1.23. Відображенням множини А в множину В називається відповідність φ: А → В (за іншою позначкою 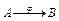 ), згідно якої кожному елементу множини А ставиться у відповідність не більш ніж один елемент множини В. Елемент b Î В називається образом елемента a Î А, а останній, у свою чергу, називається прообразом елемента b Î В.
), згідно якої кожному елементу множини А ставиться у відповідність не більш ніж один елемент множини В. Елемент b Î В називається образом елемента a Î А, а останній, у свою чергу, називається прообразом елемента b Î В.
Іншими словами, відповідність (А, В, F), де F = А ´ В, називаеться відображенням А в В, якщо область визначення відповідності збігається з її областю відправлення: Пр1 F = А.
Запись φ: А → В означає, що множина В складається з образів всіх элементів множини А (позначка образу (a) φ). Згідно означення відображення, кожному елементу b Î В (образу відповідних елементів a Î А) може відповідати один або більше елементів a Î А (прообразів відповідного елемента b Î В), а кожному елементу a Î А може відповідати не більше одного елемента b Î В, тобто відображення є однозначним. Цією обставиною клас відображень виділяється із загального класу відповідностей як частковий випадок. Помітимо, що так само як відповідність загального виду, відображення не передбачає обов’язкової участі у відповідності 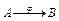 всіх елементів b Î В.
всіх елементів b Î В.
Кількість можливих відображень множини А в множину В визначити нескладно. Припустимо, що потужності множин А і В дорівнюють n і m відповідно. Побудувавши матрицю выдображення (А, В, F) розмірністю n ´ m, дійдемо висновку, що кількість можливих відображень дорівнює mn.
Означення 1.24. Відображення множини А в множину В називається сюр’єкцією, якщо для кожного b Î В існує елемент a Î А такий, що має місце відповідність aφb.
Якщо відображення φ: А → В є сюр’єкцією, то на його стрілковій діаграмі (графі) в кожну точку, що позначає елемент b Î В, входить принаймі одна стрілка і всі b Î В беруть участь у відображенні. Очевидно, що сюр’єкція множини А в множину В можлива тільки в тому випадку, якщо потужності цих множин знаходяться у співвідношенні | А |≥| В |.
Означення 1.25. Відображення множини А в множину В називається ін’єкцією, якщо різним елементам a Î А відповідають різні елементи b Î В, тобто для ai, aj Î А, ai ≠ aj мають місце відповідності aiφbi та ajφbj такі, що bi ≠ bj.
Якщо відображення φ: А → В є ін’єкцією, то на його графі в кожну точку, що позначає елемент b Î В, входить не більше ніж одна дуга. Очевидно, що ін’єкція множини А в множину В можлива тільки в тому випадку, якщо потужності цих множин знаходяться у співвідношенні | А |≤| В |.
Означення 1.26. Якщо відображення φ: А → В є одночасно сюр’єктивним і ін’єктивним, то оно називається взаємно-однозначним відображення множини А на множину В, або бієкцією А на В.
Для бієкції має виконуватись рівність | А |=| В |.
Означення 1.27. Відображення f: X → Y (або 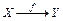 )називається функцією, якщо воно є однозначним, тобто якщо для будь-яких пар (x 1, y 1)Î f та (x 2, y 2)Î f з x 1= x 2 випливає, що y 1= y 2.
)називається функцією, якщо воно є однозначним, тобто якщо для будь-яких пар (x 1, y 1)Î f та (x 2, y 2)Î f з x 1= x 2 випливає, що y 1= y 2.
Для функції можна записати таке визначення: f ={(x, y)Î X ´ Y | y = f (x)}, тобто функцією є множина, елементами якої є пари (x, y), які беруть участь у функціональному відображенні. Значення y = f (x) для будь-якої пари (x, y)Î f називається функцією від х. Елемент x Î X називають аргументом функції y = f (x). Символичне позначення функціональної залежності y від x може бути і одним з таких: 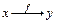 , x → y, xfy.
, x → y, xfy.
Якщо область визначення функції f містить тільки один елемент, то її називають функцією-константою.
Для задання функції використовуються такі способи: перерахуванням всіх пар (x, y) елементів множин X і Y; формулою y = f (x), x Î X, y Î Y, якщо X та Y - множини чисел (натуральних, цілих, дійсних, комплексних тощо); у вигляді графіка (x, y)Î f, x Î X, y Î Y, якщо X та Y - множини дійсних чисел.
Кількість аргументів функції (їх називають ще незалежними змінними) може бути більше одиниці. Наприклад, функція двох змінних f = f (x, y), де x Î X, y Î Y, має областю визначення декартов добуток X ´ Y. Формально таку функцію можна означити так: f ={(x, y, z)Î X ´ Y ´ Z | y = f (x, y)}. Аналогічно означаються функції більшого числа змінних. Додавання, віднімання, множення і ділення є двомісними (бінарними) функціями на R (множині дійсних чисел), тобто функціями виду f: R2 → R, або z = f (x, y),де x, y, z Î R.
Оскільки функції відносяться до класу однозначних відображень, то ім притаманні всі властивості останніх. Зокрема, функції можуть бути сюр’єктивними, ін’єктивними і бієктивними, а в останньому випадку функціональна залежність є взаємно однозначною, тобто функція f -1: Y → X, обернена до функції f: X → Y, буде також однозначною.
Композиція функцій f: X → Y і g: Y → Z визначає множину значень z Î Z, що відповідають за за послідовно застосованими законами f і g елементам x Î X: z =(g ∘ f) x = g (f (x)). Функцію f, отриману з функцій g, q, …, u підстановкою їх одне в одне з перейменуванням аргументів, називають суперпозицією функцій g, q, …, u. Наприклад, суперпозицією є функція р = f (z), де z = g (y), y = q (x), тобто р = f (g (q (x))). Вираз, що описує суперпозицію з використання символів аргументів та знакив математичних операцій, називається формулою.
Більш загальним видом відображення, ніж функція, є функціонал, який встановлює залежність між множиною чисел та множиною функцій (іншими словами – числові оцінки функцій). Приклад функціонала: 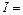
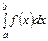 .
.
За допомогою функціоналів визначають, зокрема, цільові функції (мінімізації, максимізації функціоналу) в задачах оптимального управління динамічними системами.
Ще більш загальним видом відображення є оператор, ним встановлюється така відповідність між двома множинами функцій, що кожній функції з однієї множини відповідає певна функція з іншої. Наприклад, інтеграл Лапласа 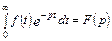 є оператором (з умовним позначенням f (t) lf (р), який здійснює інтегральне перетворення множини функцій f (t) дійсної перемінної t, 0< t <¥, у множину функцій f (р) комплексної перемінної р. Інтегральне перетворення Лапласа широко використовується в теорії автоматичного управління.
є оператором (з умовним позначенням f (t) lf (р), який здійснює інтегральне перетворення множини функцій f (t) дійсної перемінної t, 0< t <¥, у множину функцій f (р) комплексної перемінної р. Інтегральне перетворення Лапласа широко використовується в теорії автоматичного управління.
Розділ 2 Елементи математичної ЛОГІКИ
Математична логіка – це наука, предметом дослідження якої є методи логічного виведення. При цьому розглядаються форми, а не сенс суджень. Формалізація процедур логічного виведення базується на поняттях істинності та хибності посилань і висновків, причому формалізована оцінка істинності та хибності здійснюється за допомогою символів 1 та 0 відповідно, тобто в алфавіті алгебри логіки (алгебри Буля). У даному розділі розглядаються основні поняття об’єктів алгебри логіки, її закони та методи приведення логічних функцій до виду, придатного для вирішення задач побудови моделей обчислювальних і керуючих пристроїв дискретної дії.
 2015-04-23
2015-04-23 1076
1076







