Дифференциальны уравнения конвективного теплообмена

Уравнение теплопередачи. Так как при конвективном теплообмене у поверхности твердого тела всегда имеется тонкий слой теплоносителя в котором перенос тепла осуществляется только теплопроводностью, то для этого слоя можно применить закон Фурье.

Примем, что ось «y» направлена по нормали к поверхности тела, тогда

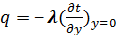, (10.3)

где условие (y = 0) означает, что рассматривается поверхность тела. С другой стороны, конвективный теплообмен описывается формулой Ньютона. Приравнивая правые части (10.1) и (10.3) найдем:

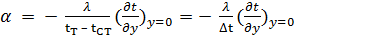(10.4)

Уравнение теплоотдачи (10.4) характеризует условие теплообмена на границе между твердым телом и теплоносителем.

Уравнение переноса тепла. Перенос тепла в неподвижной среде (твердом теле) описывается дифференциальным уравнением теплопроводности (9.15). В нем левая часть 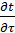представляет собой изменение температуры в фиксированном элементе тела во времени.

В движущейся среде изменение температуры частицы теплоносителя, так же, как и любой другой величины, является следствием двух обстоятельств – изменения температуры во времени и изменения ее вследствие перемещения элементов теплоносителя из одной точки пространства в другую.

Уравнение переноса тепла в движущейся среде, как и дифференциальное уравнение теплопроводности, вытекает из закона сохранения и превращения энергии и поэтому называется также дифференциальным уравнением энергии.

Переход от неподвижной среды к движущейся может быть отражен посредством замены частной (локальной) производной 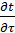на полную 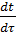. Тогда уравнение переноса тепла в движущейся среде имеет вид:

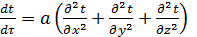; (10.5)

Оно строго верно при небольших скоростях движения газа. Раскроем величину полной производной:

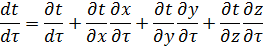
или

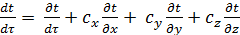(10.6)

Где с_x, с_y, с_z – проекции скорости движения на оси x, y, z.

Первый член в правой части уравнения (10.6) представляет собой скорость изменения температуры в той точке пространства, в которой находится рассматриваемый элементарный объем теплоносителя в данный момент времени, а сумма остальных членов – изменение температуры, обусловленное перемещением этого объема из одной точки пространства в другую, т.е. вследствие конвекции.

Подставляя значение 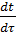из (10.6) в (10.5), получим дифференциальное уравнение энергии (переноса тепла) в движущейся среде

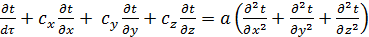(10.7)

Уравнение (10.7) можно записать и так:

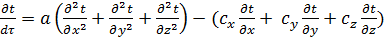(10.7’)

В правой части (10.7’) первый член определяет скорость изменения температуры в данной точке пространства вследствие переноса тепла теплопроводностью, а второй – вследствие переноса тепла конвекцией.

Конвективный теплообмен, как отмечалось, в значительной степени определяется гидродинамическими факторами. Поэтому для полного описания теплообмена в рассматриваемых условиях уравнение переноса тепла (10.7) должно быть дополнено уравнением неразрывности и уравнением движения – уравнением второго закона механики в приложении к потокам жидкости и газа – уравнением Навье–Стокса.

Система перечисленных дифференциальных уравнений описывает бесконечное множество процессов конвективного теплообмена. Чтобы выделить конкретный процесс, необходимо к ней присоединить краевые условия данного процесса (Тема 9. Вопрос 9.4). Совокупность дифференциальных уравнений и краевых условий является в принципе достаточной для решения задачи, которое обычно сводится к определению скоростей и температур, коэффициента теплопередачи и плотности теплового потока.