10.3.1 Основные понятия и определения теории подобия
Конвективный теплообмен описывается сложной системой уравнений и краевых (граничных и начальных) условий. Решение этой системы в общем случае наталкивается на большие трудности и в настоящее время получено лишь для отдельных сравнительно простых условий. Поэтому в изучении конвективного теплообмена большое значение имеет опыт. Обычно задачей опытного исследования конвективного теплообмена является отыскание зависимости коэффициента теплоотдачи от факторов, на него влияющих. Как указывалось, коэффициент α зависит от большого числа переменных. Поэтому проведение такого эксперимента сложно, ибо для выявления влияния на процесс какой-либо величины все другие следует в опыте сохранять неизменными, что не всегда возможно или затруднительно. Не меньшие трудности имеют место и при обобщении полученных результатов. Эти трудности помогает разрешить теория подобия, которая устанавливает рациональные методы постановки опыта и обобщения полученных результатов.
Теория подобия является прежде всего теоретической базой эксперимента; вместе с тем она важна и для теоретических исследований. Так, например, теория подобия указывает способы обобщения результатов численных решений уравнений, описывающих то или иное изучаемое явление. Использование теории подобия позволяет упростить и функциональные зависимости, полученные аналитическим путем.
Теория подобия – учение о подобных явлениях. Понятие подобия известны из геометрии. Это понятие может быть распространено и на физические явления. Для подобия физических явлений необходимо не только геометрическое подобие элементов систем, в которых протекают рассматриваемые явления, но и подобия величин, характеризующих эти явления (скоростей, температур, давлений, плотностей и др.).
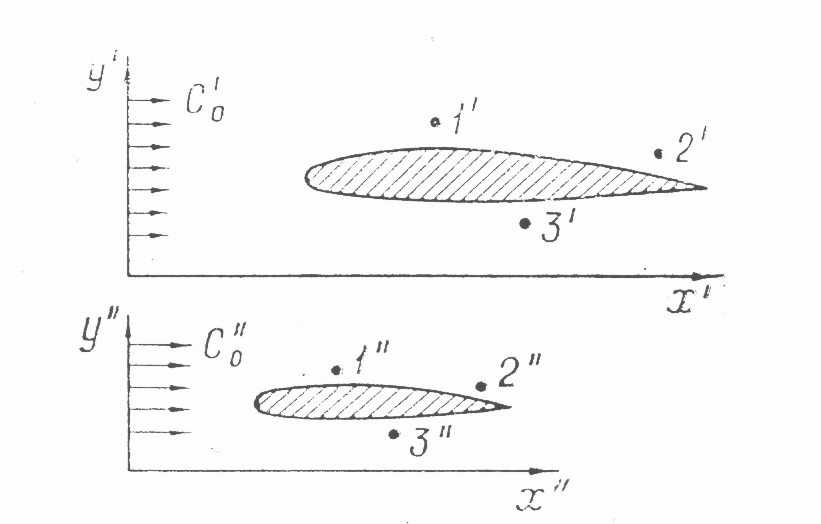
Рис. 10.3 к понятию теории подобия
Подобными называются физические явления одинаковой природы, протекающие в геометрически подобных системах при условии, что у них отношение одноименных физических величин в сходственных точках и в сходственные моменты времени одинаково. Поясним сказанное на примере. Рассмотрим два геометрически подобных тела (рис. 10.3), омываемых потоком теплоносителя с температурой T0 и скоростью с0. Выделим в этом потоке точки 1’, 2’ и 3’ и сходственные по отношению к ним точки 1”, 2” и 3”. Сходственными являются точки, координаты которых удовлетворяют геометрическому подобию. Например, для сходственных точек 1 и 1’
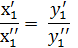
если процессы конвективного теплообмена в этих системах подобны, то у них наряду с геометрическим подобием должны быть выдержаны следующие условия:
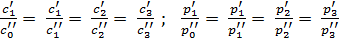 (10.8)
(10.8)
и т.д.
Здесь индексы «0», «1», «2» и «3» указывают, что рассматриваемые величины (скорость, плотность и т.д.) относятся соответственно к набегающему потоку и к точкам 1, 2, 3.
Условие (10.8) можно записать так:
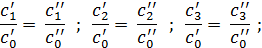
(10.9)
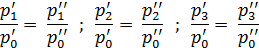
Из (10.9) следует, что в сходственных точках систем одноименные безразмерные параметры одинаковы. Это, в свою очередь, означает, что в подобных системах одинаковы (тождественны) безразмерные поля одноименных параметров.
Применение теории подобия к теплоотдачи
Критерии подобия. Критериями подобия (числами подобия) называются безразмерные комплексы, составленные из размерных величин, характеризующих данное явление. Вывод критериев подобия для каждого явления производится из анализа уравнений, описывающих это явление. Рассмотрим это на примере процесса конвективного теплообмена при стационарном движении.
Для простоты рассмотрим двухмерную задачу. Пусть имеются две подобные системы (см. рис. 10.4). в каждом из них теплообмен описывается уравнениями теплоотдачи (10.4) и переноса тепла (10.7). Приведем их к безразмерной форме. Для этого выберем масштабы приведения: для линейных величин – характерный размер l (например, длину поверхности теплообмена), для скоростей – скорость невозмущенного (набегающего) потока c0, для температур – температурный напор ΔT.
Обозначим безразмерные величины
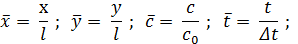
Тогда уравнения (10.4) и (10.7) с учетом того, что рассматривается стационарный процесс, принимают вид:
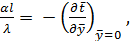 (10.10)
(10.10)
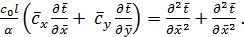 (10.11)
(10.11)
У подобных явлений, как указывалось, безразмерные поля одноименных величин тождественны. Поэтому и уравнения, их описывающие, т.е. уравнения (10.10) и (10.11), должны быть одинаковы. Последнее возможно, если каждый из безразмерных комплексов, входящих в эти уравнения, имеет одно и то же значение для всех подобных явлений, т.е.
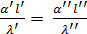 ,
, 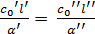 . (10.12)
. (10.12)
Здесь индексами (Ι) и (ΙΙ) обозначены величины, соответственно относящиеся к первой и второй системам (см. рис.10.3). Аналогичный анализ уравнения движения (уравнение Навье-Стокса), который мы здесь опускаем, приводит при вынужденном движении к дополнительным условиям:
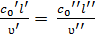 (10.13)
(10.13)
а при больших скоростях движения также к условию
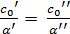 (10.13?)
(10.13?)
Безразмерные комплексы типа (10.12), 10.13) и (10.13?) являются критериями (числами) подобия. Критериям присваиваются имена выдающихся ученых, их обозначают двумя первыми буквами выбранного имени.
10.3.3 Критерии подобия процессов конвективного теплообмена.
1. Критерий Рейнольдса – 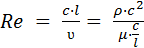
Этот критерий определяет соотношение между силами инерции и силами вязкости в потоке теплоносителя. Это следует из формулы, в которой числитель определяет силу инерции, пропорциональную скоростному напору, а знаменатель – силу вязкости (внутреннего трения). При малых числах Re преобладающими силами являются силы вязкости, при больших – силы инерции. В зависимости от соотношения этих сил меняются и условия течения жидкости, в частности режим течения; так как, при Re? Reкр – течение ламинарное, а при Re? Re кр – течение турбулентное. Таким образом, число Рейнольдса характеризует условия течения жидкости (газа) и в конечном итоге поле (распределение) скорости в потоке.
Критерий Re является определяющим критерием для конвективного теплообмена при вынужденном движении жидкости (газа), так как здесь задается скорость движения. Для процессов конвективного теплообмена при свободном движении скорость движения не задается, значит критерий Re является неопределяющим в процессах, связанных с естественной конвекцией.
2. Критерий Грасгофа – безразмерный комплекс определяется выражением:
Gr = 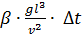
Где l – характерный линейный размер; Δt = (tст – tж); β – коэффициент объемного расширения при нагревании в 1К; для идеального газа β = 1/Т
Критерий Грасгофа характеризует интенсивность свободного движения, которая зависит от соотношения между подъемной силой, обусловленной различием плотности в отдельных точках изотермического потока, и сил вязкого трения. Этот критерий является определяющим в процессах, связанных с естественной конвекцией.
3. Критерий Прандтля составлен из физических параметров вещества и является физическим параметром.
Pr = 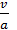
Данный критерий характеризует соотношение между скоростью обмена механической энергией между частицами жидкости (за счет вязкости) и скоростью обмена тепловой энергией (за счет температуропроводности – а). Критерий Pr – критерий физических средств вещества и является определяющим критерием. Для некоторых капельных жидкостей (вода, масло, глицерин) с ростом температуры в величина Pr сильно уменьшается. Критерий Прандтля жидких металлов меняется в пределах Pr = 0,005…0,05; также жидкие значения критерия Pr жидких металлов в основном объясняются их высокой теплопроводностью. Многим нефтепродуктам свойственны, наоборот, высокие значения Pr из-за высокой вязкости.
Для газов значение критерия Прандтля практически не зависит от температуры, а зависит только от числа атомов в молекуле:
- для одноатомных газов Pr = 0,65;
- для двухатомных газов Pr = 0,72;
- для трехатомных газов Pr = 0,8;
- для многоатомных газов Pr = 1,0;
4. Критерий Пекле – безразмерный комплекс определятся выражением:
Pe = 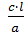 ,
,
Где а – коэффициент температуропроводности. Представим критерий Пекле следующим образом:
Pe = 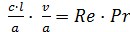
Где Pr = v/а – Критерий Грандтля;
Re = c·l/v – критерий Рейнольдса.
4. Критерий Нуссельта –
Nu = 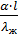
Этот критерий представляет собой безразмерный коэффициент теплоотдачи и характеризует соотношение между интенсивностью теплоотдачи α, и интенсивностью теплопроводности в пограничном слое потока жидкости (λж). Коэффициент теплоотдачи α всегда является величиной искомой, неизвестной в задачах о конвективном теплообмене. Следовательно, критерий Nu является неопределяющим критерием и его значение всегда зависит от значения всех определяющих критериев
Nu = f (Re, Gr, Pr).
Это уравнение называется критериальным уравнением конвективного теплообмена. Обычно из двух гидродинамических критериев Re и Gr в уравнении останется лишь один:
- при естественной конвекции – критерий Gr;
- при вынужденной конвекции - критерий Re;
6. Критерий Маха – M = 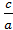
Характеризует сжимаемость газового потока; поэтому его изменение влияет на процессы теплообмена при значениях М, когда эта сжимаемость ощутима.
10.3.4. Теоремы подобия
Первая теорема подобия ( Теорема Ньютона). Первая теорема подобия формулируется так:
У подобных явлений одноименные критерии подобия численно одинаковы. Следовательно, в подобных процессах конвективного теплообмена при вынужденном движении критерии Nu, Pe, Re, M этих подобных процессов имеют численно одинаковые значения. Данное условие записывается так:
Nu = idem, Pe = idem, Re = idem, M = idem (10.14)
Имея в виду, что Pe = Re · Pr, условие (10.14) можно заменить условием
Nu = idem, Pr = idem, Re = idem, M = idem (10.15)
В отдельных частных случаях условия подобия упрощаются. Например, при малых скоростях движений газа (Mio, 3), когда можно пренебречь сжимаемостью газа, отпадает условие M = idem.
Поэтому подобные процессы конвективного теплообмена при малых скоростях движения характеризуются условием
Nu = idem, Re = idem, Pr = idem (10.16)
Таким образом, равенство одноименных критериев подобия является следствием подобия явлений. Вместе с тем, это обстоятельство может служить и признаком по которому устанавливается наличие или отсутствие подобия физических явлений.
Вторая теорема подобия. Выше отмечалось, что теория подобия позволяет решать вопрос о рациональном обобщении результатов исследований. Решение этой задачи базируется на второй теореме подобия. Согласно этой теореме решение системы уравнений, описывающих какое-либо явление, может быть представлено в виде зависимости между критериями подобия, получаемыми из данной системы уравнений.
Рассмотрим это положение на примере конвективного теплообмена. Введем в (10.10) и (10.11) критерии подобия, тогда
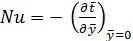 (10.17)
(10.17)
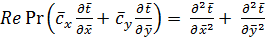 (10.18)
(10.18)
Таким образом, конвективный теплообмен описывается безразмерными уравнениями (10.17) и (10.18), в которых безразмерные величины можно рассматривать как новые переменные; их две группы:
- независимые, составленные только из заданных размерных величин: Re, Pr, 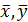 ;
;
- зависимые, включающие в себя искомые величины: Nu, 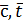 .
.
Критерии подобия, являющиеся независимыми переменными (Re, Pr и др.), называют определяющими критериями, а зависимые – определяемыми.
Очевидно, что искомая (определяемая) величина является функцией независимых (определяющих) величин, входящих в систему уравнений. Поэтому на основе сказанного можно записать
Nu = f (Re, Pr, 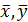 ). (10.19)
). (10.19)
А для заданной точки пространства –
Nu = f (Re, Pr). (10.20)
Уравнения (10.19) и (10.20), представляющие собой функциональную связь между критериями подобия, называются уравнения подобия (критериальными уравнениями). В частности, уравнения (10.19) и (10.20) представляют собой уравнения подобия стационарного конвективного теплообмена при вынужденном движении.
Таким образом, мы показали, что результаты исследований можно представить в виде уравнений подобия, а не только в виде функциональной связи между размерными величинами. Число критериев подобия меньше числа размерных величин, из которых они составлены. Поэтому число независимых переменных в уравнениях подобия меньше, чем в уравнениях, выражающих связь между размерными величинами, характеризующими процесс. Следовательно, результаты исследования конвективного теплообмена при вынужденном движении можно представить в виде зависимости (10.20). Если бы результаты такого исследования представлялись в виде функциональной зависимости между размерными величинами, характеризующими данный процесс, то полученное уравнение должно было бы иметь вид (10.2). Сравнение (10.2 и 10.20) позволяет сделать вывод, что использование критериальных уравнений подобия существенно упрощает постановку исследований и их обобщение.
 2015-04-23
2015-04-23 24194
24194
