При лучистом теплообмене тепловая энергия, в результате сложных внутриатомных возмущений на поверхности одного тела, превращается в лучистую, а затем на поверхности другого тела происходит обратный процесс превращения лучистой энергии в тепловую. Интенсивность переноса тепла определяется температурами, состоянием и цветом поверхностей тел, их взаимным расположением, характером разделяющей среды и др. Лучистая энергия представляет собой световые (длина волны 0,4...0,8m) и инфракрасные, или тепловые (длина волны 0,8...40m), электромагнитные волны. Если система тел имеет одинаковую температуру, то она находится в динамическом тепловом равновесии, при котором количество излучаемой и поглощаемой лучистой энергии для каждого тела одинаково.
Лучистый поток, падающий на тело Qo,, разделяется на поглощенный Qa, отраженный Qr и проходящий сквозь тело Qd.
Qo=Qa+Qr+Qd, или A+R+D=1, (2.46)
где A=Qa/Qo, R=Qr/Qo и D=Qd/Qo – поглощательная, отражательная и пропускательная способности тела.
В зависимости от соотношения параметров A, R и D тела подразделяются на абсолютно черное, абсолютно белое, зеркальное, диатермическое и серое.
При R=0, A=1 и D=0 вся падающая лучистая энергия поглощается телом и превращается в тепловую. Тело будет абсолютно черным. В природе таким телом является космическое пространство.
При R=1, A=0 и D=0 вся падающая лучистая энергия полностью телом отражается. Тело будет зеркальным (если отражение следует законам оптики) или абсолютно белым (если отражение будет диффузионным). В природе таких тел не существует.
При R=0, A=0 и D=1 вся падающая лучистая энергия проходит через тело. Тело будет абсолютно прозрачным (проницаемым). В природе таким телом является безвоздушное пространство, а для тепловых лучей – также газы с неполярными молекулами.
При R¹0, A¹0 и D¹1 падающая лучистая энергия частично проходит через тело, частично поглощается и частично отражается. Тело будет серым. Практически все тела в природе являются серыми.
Значения A, R и D в первую очередь зависят от природы тела, затем от длины волны и температуры. Большинство твердых тел и жидкостей имеют нулевую пропускательную способность. Кварц не пропускает тепловые лучи, а для световых и ультрафиолетовых он прозрачен. Стекло прозрачно для световых лучей и практически не пропускает тепловые и ультрафиолетовые лучи. Поваренная соль хорошо пропускает тепловые лучи, но плохо – световые. Белая поверхность хорошо отражает световые лучи, а тепловые лучи она поглощает почти так же, как и поверхности темных цветов. Для поглощения и отражения тепловых лучей важен не столько цвет, сколько состояние поверхности. Независимо от цвета отражательная способность полированных поверхностей многократно выше, чем шероховатых.
Количество энергии, излучаемое единицей поверхности тела, называется лучеиспускательной способностью тела Е (Вт/м2), а лучеиспускательная способность определённой длины волны называется спектральной интенсивностью излучения Il=dE/dl (Вт/м3).
Согласно закону Планка интенсивность излучения для волн с длиной волны l определяется выражением
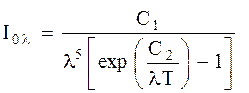 , (2.47)
, (2.47)
где С1 и С2 – константы; l – длина волны, м; T – температура, К.
Для каждой температуры интенсивность излучения растет от нулевых значений при l=0 до максимального при длине волны lm и вновь уменьшается до нуля при l=¥. Чем выше температура, тем короче длина волны lm, что устанавливается законом Вина
lmT=0,0029. (2.48)
Полное количество лучистой энергии, излучаемой во всем спектре волн, называется интегральным излучением и представляет собой лучеиспускательную способность абсолютно черного тела. Согласно закону Стефана-Больцмана лучеиспускательная способность абсолютно черного тела пропорциональна абсолютной температуре в четвертой степени
Eo=òEol dl=soT4=Co(T/100)4, (2.49)
где sо=5,67×10-8 Вт/(м2×К4) – константа излучения абсолютно черного тела; Со=5,67 Вт/(м2×К4) – коэффициент лучеиспускания абсолютно черного тела.
Серые тела имеют меньшую лучеиспускательную способность. Отношение коэффициентов лучеиспускания серого тела к лучеиспускательной способности абсолютно черного тела называют степенью черноты тела
e=С/Со. (2.50)
В соответствии с законом Кирхгофа отношение лучеиспускательной способности к поглощательной способности для всех тел одинаково и зависит только от температуры
С1/А1=С2/А2=...=Со/Ао=const. (2.51)
Из закона Кирхгофа следует, что поглощательная способность тела равна его степени черноты при той же температуре.
Количество тепла, передаваемое от горячего тела к холодному при их произвольном расположении в прозрачной среде, определяется выражением
Q1-2=e1-2Co((T1/100)4-(T2/100)4)j1-2Fp, (2.52)
где e1-2=e1e2 – приведенная степень черноты системы тел; Т1 и Т2 – температуры горячей и холодной поверхностей, соответственно, К; Fр – условная расчетная поверхность, м2; j1-2 - угловой коэффициент;
j1-2=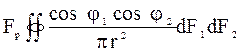 ;
;
где j1 и j2 – углы падения тепловых лучей, рад; r – расстояние между телами, м.
Для частных случаев уравнение (2.52) упрощается. Например, для замкнутой системы двух серых тел
Q1-2=eпрCo[(T1/100)4–(T2/100)4]Н, (2.53)
где enр=1/[(1/e1-0,5)j1-2+(1/e2-0,5)j2-1] – приведенная степень черноты; Н=F1j1-2=F2j2-1 – приведенная поверхность теплоотдачи, м2; j1-2 и j2-1 – средние по поверхности угловые коэффициенты излучения тела 1 на тело 2 и наоборот.
Формулы для расчета угловых коэффициентов приводятся в справочной литературе. Если тело 1 не имеет вогнутостей и находится внутри тела 2, то j1-2=1; j2-1=F1/F2 и Н=F1. Для параллельных поверхностей eпр=1/S(1/ei-0,5). При теплообмене между двумя пластинами в знаменателе будут два слагаемых, а при установке между ними третьей пластины (экрана) в теплообмене будут участвовать уже четыре поверхности и в знаменателе будут четыре слагаемых.
Для уменьшения лучистого теплового потока между излучающими поверхностями устанавливают экраны. Установка между двумя пластинами с одинаковой степенью черноты третьей с той же степенью черноты уменьшает поток в два раза, а установка n экранов снижает лучистый тепловой поток в 1/(n+1) раз. Если экран будет абсолютно черным, то тепловой поток не изменится. Установка полированного экрана может уменьшить лучистый тепловой поток практически до нуля.
Экраны могут быть использованы также для снижения температур лучеиспускающих поверхностей, омываемых газообразным теплоносителем. Так, установка бумажного экрана между двумя параллельными пластинами, охлаждаемыми воздухом, будет равносильна увеличению поверхности теплоотдачи вдвое, и соответственно снижает в два раза температурный напор.
Газы, в отличие от тел, излучают и поглощают лучистую энергию всем объемом. Кроме того, газы имеют линейчатые спектры, т.е. они излучают и поглощают лучи определённых длин волн. Тепловые лучи излучают только газы с полярными молекулами. Обычно это водяные пары и углекислый газ.
Количество тепла, перераспределяемое между холодным телом с поверхностью F и окружающим его горячим газом, определяется зависимостью
Q=eс¢Co[eг(Tг/100)4-Аг(Tс/100)4]F, (2.54)
где eс¢=(eс+1)/2 – приведенная степень черноты стенки; eг=eу.г+beв – степень черноты газа при температуре Тг; Аг – коэффициент излучения газа, который определяется так же, как и степень черноты, но при температуре стенки; eуг, eв и b – степень черноты углекислого газа, водяных паров и поправочный коэффициент для водяного пара на его парциальное давление. Поправочный коэффициент определяется по справочным номограммам в зависимости от температуры и произведения парциального давления на эффективную длину пути тепловых лучей. Длина пути находится как отношение учетверенного объема газа к поверхности тела. Если выражение в скобках принимает отрицательное значение, то это означает, что газ не отдает, а воспринимает тепловую энергию. При неограниченном объеме газа можно принимать eг=1 и Аг=1.
Сложный теплообмен наблюдается при конвективном теплообмене в газах, когда тепло одновременно передается конвекцией и лучистым теплообменом. При этом общее количество тепла определяется суммой Q=Qк+Qл. После подстановки значений конвективного теплового потока по уравнению (2.17) и лучистого теплового потока по формуле (2.54) получим
Q=aÑt F+eс¢Co[eг(Tг/100)4-Аг(Tс/100)4)F=(a+aл)Ñt F, (2.55)
где aл=eс¢Co[eг(Tг/100)4-Аг(Tс/100)4]/Ñt – коэффициент теплоотдачи лучистого теплообмена, Вт/(м2×К).
Обычно сумму коэффициентов теплоотдачи называют коэффициентом теплоотдачи сложного теплообмена aсл=a+aл. Для наиболее часто встречающегося сложного теплообмена между горячей стенкой и воздухом коэффициент теплоотдачи сложного теплообмена в Вт/(м2гр) определяют по эмпирическому уравнению
aсл=9,74+0,07Ñt. (2.56)
Уравнение (2.56) обычно используется для определения тепловых потерь стенками аппаратов. При необходимости получения более точных значений применяют соответствующие зависимости для определения конвективного и лучистого коэффициентов теплоотдачи.
Расчет теплопотерь обычно проводят по удельным тепловым потерям. В этом случае температурный перепад неизвестен. Совместное решение формулы (2.56) и уравнения q=aÑt дает формулу для коэффициента теплоотдачи через удельный тепловой поток
aсл=9,74/(1-0,07/q). (2.57)
Таблица 11.1
Степень черноты полного нормального излучения для различных материалов
| Наименование материала | t,°С | e |
| Алюминий полированный | 50—500 | 0,04—0,06 |
| Бронза | 0,1 | |
| Железо листовое оцинкованное, блестящее | 0,23 | |
| Жесть белая, старая | 0,28 | |
| Золото полированное | 200 - 600 | 0,02—0,03 |
| Латунь матовая | 20-350 | 0,22 |
| Медь полированная | 50—100 | 0,02 |
| Никель полированный | 200—400 | 0,07—0,09 |
| Олово блестящее | 20—50 | 0,04—0,06 |
| Серебро полированное | 200—600 | 0,02—0,03 |
| Стальной листовой прокат | 0,56 | |
| Сталь окисленная | 200—600 | 0,8 |
| Сталь сильно окисленная | 0,98 | |
| Чугунное литье | 0,81 | |
| Асбестовый картон | 0,96 | |
| Дерево строганое | 0,8—0,9 | |
| Кирпич огнеупорный | 500—1000 | 0,8—0,9 |
| Кирпич шамотный | 0,75 | |
| Кирпич красный, шероховатый | 0,88—0,93 | |
| Лак черный, матовый | 40—100 | 0,96—0,98 |
| Лак белый | 40—100 | 0:8—0,95 |
| Масляные краски различных цветов... | 0,92—0,96 | |
| Сажа ламповая | 20—400 | 0,95 |
| Стекло | 20—100 | 0,91—0,94 |
| Эмаль белая | 0,9 |
Закон Кирхгофа. Для всякого тела излучательная и поглощательная способности зависят от температуры и длины волны. Различные тела имеют различные значения Е и А. Зависимость между ними устанавливается законом Кирхгофа:
Е = Еs*А или Е /А = Еs = Еs/Аs = Сs*(Т/100)4. (11.11)
Отношение лучеиспускательной способности тела (Е) к его погло-щательной способности (А) одинаково для всех серых тел, находящихся при одинаковых температурах и равно лучеиспускательной способности абсолютно черного тела при той же температуре.
Из закона Кирхгофа следует, что если тело обладает малой поглощательной способностью, то оно одновременно обладает и малой лучеиспускательной способностью (полированные металлы). Абсолютно черное тело, обладающее максимальной поглощательной способностью, имеет и наибольшую излучательную способность.
Закон Кирхгофа остается справедливым и для монохроматического излучения. Отношение интенсивности излучения тела при определенной длине волны к его поглощательной способности при той же длине волны для всех тел одно и то же, если они находятся при одинаковых температурах, и численно равно интенсивности излучения абсолютно черного тела при той же длине волны и температуре, т.е. является функцией только длины волны и температуры:
Еl / Аl = Il / Аl = Еsl = Isl = f (l,T). (11.12)
Поэтому тело, которое излучает энергию при какой-нибудь длине волны, способно поглощать ее при этой же длине волны. Если тело не поглощает энергию в какой-то части спектра, то оно в этой части спектра и не излучает.
Из закона Кирхгофа также следует, что степень черноты серого тела е при одной и той же температуре численно равно коэффициенту поглощения А:
e = Il / Isl = Е/ Еsl = C / Csl = А. (11.13)
Закон Ламберта. Излучаемая телом лучистая энергия распространяется в пространстве по различным направлениям с различной интенсивностью. Закон, устанавливающий зависимость интенсивности излучения от направления, называется законом Ламберта.
Закон Ламберта устанавливает, что количество лучистой энергии, излучаемое элементом поверхности dF1 в направлении элемента dF2, пропорционально произведению количества энергии, излучаемой по нормали dQn, на величину пространственного угла dщ и csц, составленного направлением излучения с нормалью (рис.11.2):
d2Qn = dQn*dw*csj. (11.14)
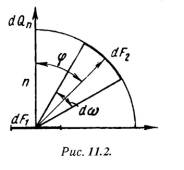
Следовательно, наибольшее количество лучистой энергии излучается в перпендикулярном направлении к поверхности излучения, т. е. при (j = 0). С увеличением j количество лучистой энергии уменьшается и при j = 90° равно нулю. Закон Ламберта полностью справедлив для абсолютно черного тела и для тел, обладающих диффузным излучением при j = 0 - 60°.
Для полированных поверхностей закон Ламберта неприменим. Для них лучеиспускание при угле j будет большим, чем в направлении, нормальном к поверхности.
 2014-02-02
2014-02-02 1024
1024








