Построение графика функции 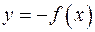
по графику функции 
Функции  и
и 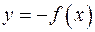 имеют одну и ту же область определения. График функции
имеют одну и ту же область определения. График функции 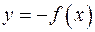 может быть получен из графика функции
может быть получен из графика функции  симметричным отображением графика функции
симметричным отображением графика функции  относительно оси Ох.
относительно оси Ох.
Пример. Построим график функции 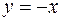 по графику функции
по графику функции 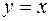 .
.
Решение. Построим график вспомогательной функции 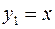 . Построим график функции
. Построим график функции 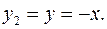 Для этого симметрично отобразим график функции
Для этого симметрично отобразим график функции  относительно оси Ох (Рис. 61).
относительно оси Ох (Рис. 61).
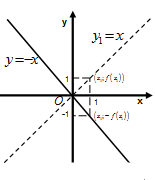
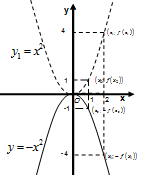
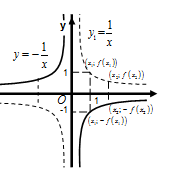
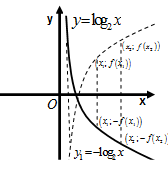
Аналогично строят графики функций 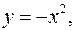 (Рис. 62),
(Рис. 62), 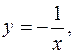 (Рис. 63),
(Рис. 63), 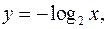 (Рис. 64).
(Рис. 64).
Построение графиков функции 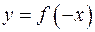
по графику функции 
Функции  и
и 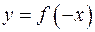 имеют области определения симметричные относительно начала координат. График функции
имеют области определения симметричные относительно начала координат. График функции 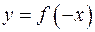 может быть получен из графика функции
может быть получен из графика функции  симметричным отображением последнего относительно оси Оу. Графики функций
симметричным отображением последнего относительно оси Оу. Графики функций  и
и 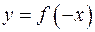 состоят из попарно симметричных относительно оси Оу точек
состоят из попарно симметричных относительно оси Оу точек 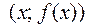 и
и 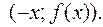
Пример. Построим график функции 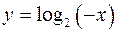 по графику функции
по графику функции 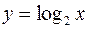 .
.
Решение. Построим график вспомогательной функции 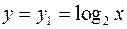 (Рис. 65). Симметрично отобразим график функции
(Рис. 65). Симметрично отобразим график функции 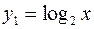 относительно оси Оу.
относительно оси Оу.
Аналогично строят график функции 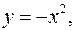 (Рис. 66).
(Рис. 66).
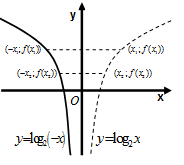
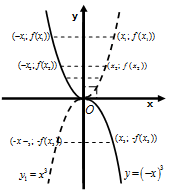
Рис. 65 Рис. 66
Построение графика функции 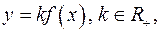
по графику функции 
Функции  и
и 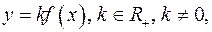 имеет одну и ту же область определения. Ординаты графика функции
имеет одну и ту же область определения. Ординаты графика функции 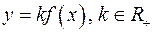 могут быть получены умножением ординат графика функции
могут быть получены умножением ординат графика функции  на одно и то же число k >0.
на одно и то же число k >0.
Такое преобразование графика функции  называют растяжением.
называют растяжением.
Если k >1, то точку 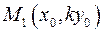 получают из точки
получают из точки 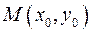 растяжением ординаты точки М в
растяжением ординаты точки М в 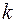 раз.
раз.
График функции 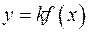 может быть получен из графика функции
может быть получен из графика функции  растяжением в
растяжением в 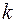 раз вдоль оси Оу графика функции
раз вдоль оси Оу графика функции  .
.
Если 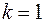 , то все точки графика
, то все точки графика  остаются на месте.
остаются на месте.
Если 0< k< 1, то точку 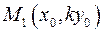 получают из точки
получают из точки 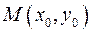 сжатием ординаты точки
сжатием ординаты точки 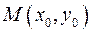 в
в 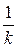 раз и график функции
раз и график функции 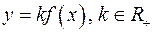 получают из графика функции
получают из графика функции  сжатием ординат всех точек в
сжатием ординат всех точек в 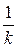 раз, то есть сжатием в
раз, то есть сжатием в 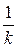 раз вдоль оси Оу графика функции
раз вдоль оси Оу графика функции  .
.
Пример. Построим этим способом график функции 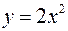 (Рис. 67).
(Рис. 67).
Решение. Сначала строим график функции 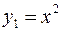 , затем ординаты всех точек графика функции
, затем ординаты всех точек графика функции 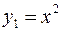 умножаем на 2.
умножаем на 2.
Построим данным способом график функции 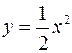 (Рис. 68).
(Рис. 68).
Для построения графика функции 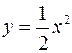 строим график функции
строим график функции 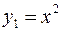 , затем ординаты всех точек графика функции
, затем ординаты всех точек графика функции 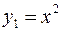 умножаем на
умножаем на 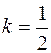 (Рис. 69). То есть график функции
(Рис. 69). То есть график функции 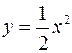 получают сжатием вдоль оси Оу в
получают сжатием вдоль оси Оу в 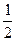 раз графика функции
раз графика функции 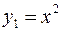 .
.
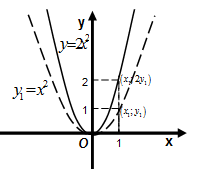
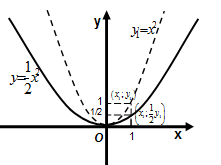
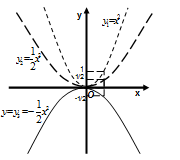 Рис. 70
Рис. 70
Рис. 68 Рис. 69
Пример. Построим график функции 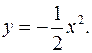
Решение. Строим график вспомогательной функции 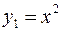 , затем ординаты всех точек графика функции
, затем ординаты всех точек графика функции 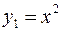 умножаем на
умножаем на 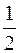 , получим график второй вспомогательной функции
, получим график второй вспомогательной функции 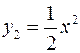 (Рис. 70). Строим график функции
(Рис. 70). Строим график функции 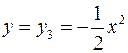 , для этого симметрично отобразим график функции
, для этого симметрично отобразим график функции 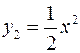 относительно оси Ох.
относительно оси Ох.
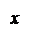 Построение графика функции
Построение графика функции 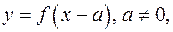
по графику функции 
Функция 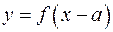 определена для всех тех х, для которых
определена для всех тех х, для которых 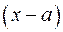 принадлежит области определения функции
принадлежит области определения функции  . Каждую точку графика функции
. Каждую точку графика функции 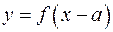 получают из соответствующей точки графика функции
получают из соответствующей точки графика функции  сдвигом графика функции
сдвигом графика функции  , как жесткого тела, вдоль оси Ох на величину а. При этом, если a >0, то сдвиг производят вправо на величину а (Рис. 71 а), если а <0, то сдвиг производят влево на величину | а | (Рис. 71 б).
, как жесткого тела, вдоль оси Ох на величину а. При этом, если a >0, то сдвиг производят вправо на величину а (Рис. 71 а), если а <0, то сдвиг производят влево на величину | а | (Рис. 71 б).
Пример. Построим график функции 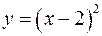 и
и 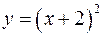 по графику функции
по графику функции 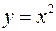 .
.
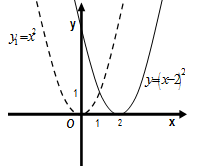
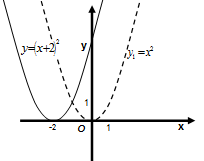
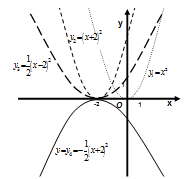 Рис. 72
Рис. 72
а) Рис. 71 б)
Решение. Строим график вспомогательной функции 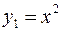 . Для построения графика функции
. Для построения графика функции 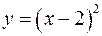 осуществляем сдвиг графика функции
осуществляем сдвиг графика функции 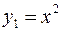 , как жесткого тела, вдоль оси Ох на два единичных отрезка вправо. Для построения графика функции
, как жесткого тела, вдоль оси Ох на два единичных отрезка вправо. Для построения графика функции 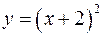 осуществляем сдвиг графика функции
осуществляем сдвиг графика функции 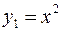 , как жесткого тела, вдоль оси Ох на два единичных отрезка влево. (Рис.).
, как жесткого тела, вдоль оси Ох на два единичных отрезка влево. (Рис.).
Пример. Построим график функции 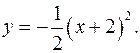
Решение. Сначала строим график вспомогательной функции 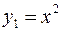 . Для построения графика функции
. Для построения графика функции 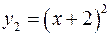 осуществляем сдвиг графика функции
осуществляем сдвиг графика функции 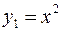 , как жесткого тела, вдоль оси Ох на два единичных отрезка влево (Рис. 72). Затем ординаты всех точек графика функции
, как жесткого тела, вдоль оси Ох на два единичных отрезка влево (Рис. 72). Затем ординаты всех точек графика функции 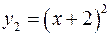 умножаем на
умножаем на 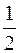 , получим график третьей вспомогательной функции
, получим график третьей вспомогательной функции 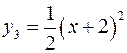 . Строим график функции
. Строим график функции 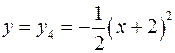 , для этого симметрично отобразим график функции
, для этого симметрично отобразим график функции 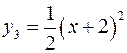 относительно оси Ох.
относительно оси Ох.
Построение графика функции 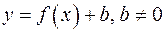
по графику функции 
Функции 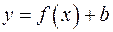 и
и  имеют одну и ту же область определения. Чтобы получить некоторую точку М1, принадлежащую графику функции
имеют одну и ту же область определения. Чтобы получить некоторую точку М1, принадлежащую графику функции 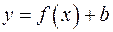 , необходимо точку М0, принадлежащую графику функции
, необходимо точку М0, принадлежащую графику функции  , сдвинуть вдоль оси Оу на величину
, сдвинуть вдоль оси Оу на величину 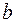 . При этом, если
. При этом, если 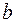 >0, то сдвиг производят на величину вверх
>0, то сдвиг производят на величину вверх 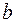 по оси Оу. Если
по оси Оу. Если 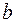 <0, то сдвиг производят вниз на величину |
<0, то сдвиг производят вниз на величину | 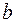 |.
|.
Пример. Построим график функции график функции 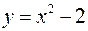 (Рис. 33) и
(Рис. 33) и 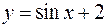 , (Рис. 73).
, (Рис. 73).
Решение. Строим график вспомогательной функции 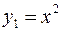 . Для построения графика функции
. Для построения графика функции 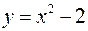 осуществляем сдвиг графика функции
осуществляем сдвиг графика функции 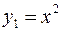 , как жесткого тела, вдоль оси Оу на два единичных отрезка вниз. Для построения графика функции
, как жесткого тела, вдоль оси Оу на два единичных отрезка вниз. Для построения графика функции 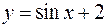 осуществляем сдвиг графика функции
осуществляем сдвиг графика функции 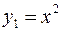 , как жесткого тела, вдоль оси Оу на два единичных отрезка вверх (Рис. 74).
, как жесткого тела, вдоль оси Оу на два единичных отрезка вверх (Рис. 74).
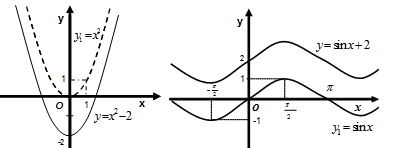
Рис. 73 Рис. 74
 2015-04-23
2015-04-23 681
681







