Пример 1. Проведем исследование функции 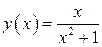 и построим эскиз ее графика.
и построим эскиз ее графика.
Решение. Область определения функции 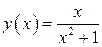 :
: 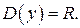
Найдем множество значений функции  .
.
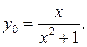 Если
Если 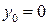 , то уравнение
, то уравнение 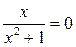 имеет единственный корень
имеет единственный корень 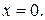 Значит график функции проходит через начало координат и
Значит график функции проходит через начало координат и 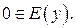
Пусть 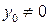 , тогда
, тогда 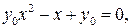
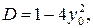
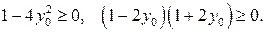
Следовательно, 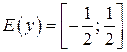 . При этом наибольшее значение функции равно
. При этом наибольшее значение функции равно 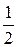 , в точке
, в точке 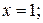 наименьшее значение функции равно
наименьшее значение функции равно 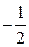 , в точке
, в точке 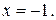 Точки
Точки 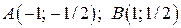 принадлежат графику функции
принадлежат графику функции 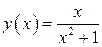 . Данная функция по определению ограничена сверху и снизу и, следовательно, ограничена.
. Данная функция по определению ограничена сверху и снизу и, следовательно, ограничена.
Исследуем функцию 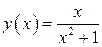 на четность:
на четность:
− область определения функции  симметричное относительно начала координат множество;
симметричное относительно начала координат множество;
− 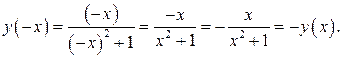
Следовательно, функция 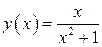 нечетная по определению.
нечетная по определению.
График данной функции симметричен относительно начала координат, его можно построить для 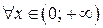 , а затем симметрично отразить относительно начала координат.
, а затем симметрично отразить относительно начала координат.
Функция 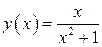 непериодическая.
непериодическая.
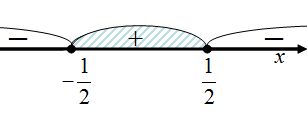
Определим промежутки знакопостоянства данной функции:
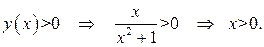 То есть
То есть 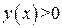 , при
, при 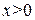 ;
; 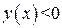 , при
, при 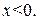 График данной функции лежит выше оси
График данной функции лежит выше оси 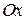 при
при 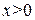 , ниже оси
, ниже оси 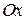 при
при 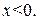
Определим промежутки монотонности функции 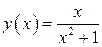 .
.
Пусть 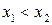 . Сравним
. Сравним 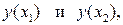 где
где 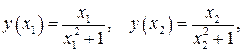 имеем
имеем
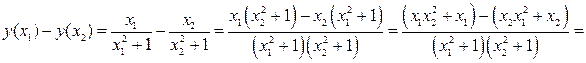
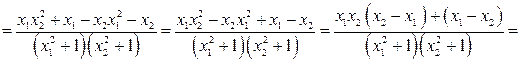
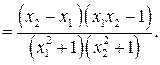 Установим знак выражения
Установим знак выражения 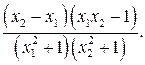
По условию 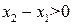 , выражение
, выражение 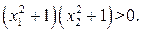 Определим знак выражения
Определим знак выражения 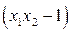 . Для этого заменим
. Для этого заменим 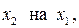 имеем:
имеем: 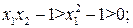
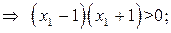

Следовательно, на 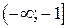 и на
и на 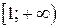
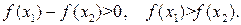 Таким образом, на
Таким образом, на 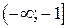 и на
и на 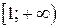 функция
функция 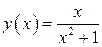 убывает.
убывает.
Аналогично, на 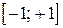 функция
функция 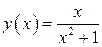 возрастает.
возрастает.
Следовательно, 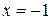 – точка минимума функции
– точка минимума функции 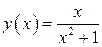 ;
; 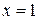 – точка максимума функции
– точка максимума функции 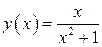 .
.
Точка 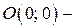 единственная точка пересечения с осями координат.
единственная точка пересечения с осями координат.
Эскиз графика функции 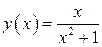 приведен на рисунке 87.
приведен на рисунке 87.
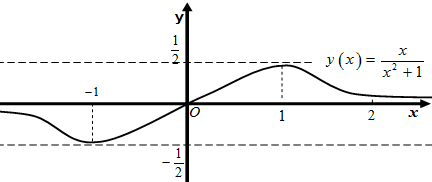
Рис. 87
Пример 2. Проведем исследование функции 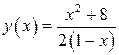 и построим эскиз ее графика.
и построим эскиз ее графика.
Решение. Определим область определения функции 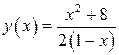 :
: 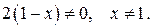 Следовательно,
Следовательно, 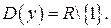
Найдем множество значений функции 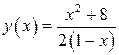 .
.
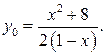 Если
Если 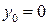 , то уравнение
, то уравнение 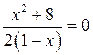 не имеет корней. Значит график функции не пересекает ось
не имеет корней. Значит график функции не пересекает ось 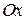 .
.
Пусть 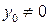 , тогда
, тогда 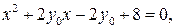
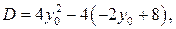
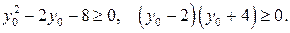
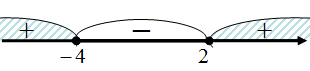
Следовательно, 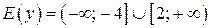 . При этом ни наибольшего, ни наименьшего значения функция не имеет. Значение
. При этом ни наибольшего, ни наименьшего значения функция не имеет. Значение 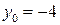 функция принимает при
функция принимает при 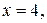 значение
значение 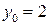 функция принимает при
функция принимает при 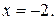 Точки
Точки 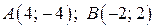 принадлежат графику функции
принадлежат графику функции 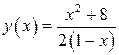 . Данная функция не ограничена ни сверху, ни снизу и, следовательно, не ограничена. На интервале
. Данная функция не ограничена ни сверху, ни снизу и, следовательно, не ограничена. На интервале 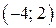 нет ни одной точки графика функции.
нет ни одной точки графика функции.
При 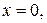
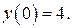
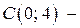 точка пересечения графика функции
точка пересечения графика функции 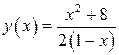 с осью
с осью 
Исследуем функцию 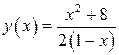 на четность. Область определения функции
на четность. Область определения функции 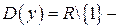 не симметричное относительно начала координат множество, следовательно
не симметричное относительно начала координат множество, следовательно 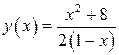 функция общего вида.
функция общего вида.
Функция 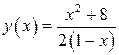 непериодическая.
непериодическая.
Определим промежутки знакопостоянства данной функции:
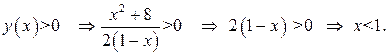 То есть
То есть 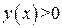 , при
, при 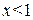 ;
; 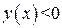 , при
, при 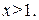 График данной функции лежит выше оси
График данной функции лежит выше оси 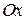 при
при 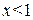 , ниже оси
, ниже оси 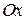 при
при 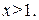
Определим промежутки монотонности функции 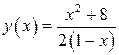 .
.
Пусть 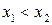 . Сравним
. Сравним 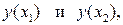 где
где 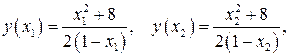 имеем
имеем
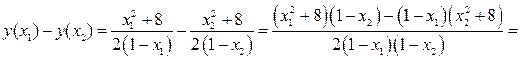
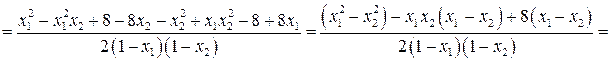
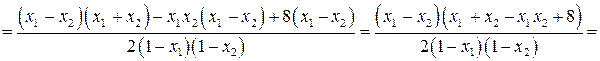
Установим знак выражения 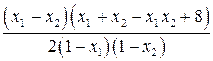 .
.
По условию 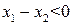 . Определим знак выражения
. Определим знак выражения 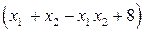 . Для этого заменим
. Для этого заменим 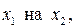 имеем:
имеем: 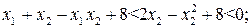
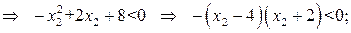
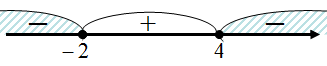
Определим знак выражения 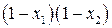 .
. 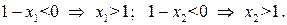
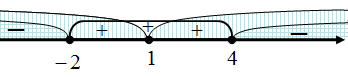
Следовательно, на 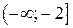 и на
и на 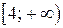
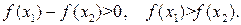 Таким образом, на
Таким образом, на 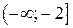 и на
и на 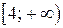 функция
функция 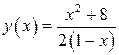 убывает.
убывает.
Аналогично, на 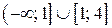 функция
функция 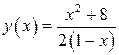 возрастает.
возрастает.
Следовательно, 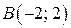 – точка минимума функции
– точка минимума функции 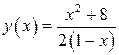 ;
; 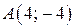 – точка максимума функции
– точка максимума функции 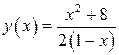 .
.
Эскиз графика функции 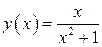 приведен на рисунке 88.
приведен на рисунке 88.
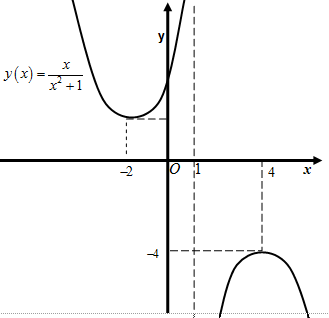
Рис. 88
Пример 3. Проведем исследование функции 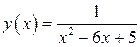 и построим эскиз ее графика.
и построим эскиз ее графика.
Решение. Определим область определения функции 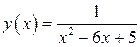 :
: 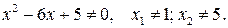
Следовательно, 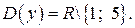
Найдем множество значений функции 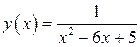 .
.
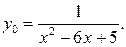 Если
Если 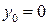 , то уравнение
, то уравнение 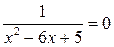 не имеет корней. Значит график функции не пересекает ось
не имеет корней. Значит график функции не пересекает ось 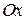 .
.
Пусть 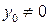 , тогда
, тогда 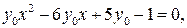
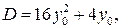
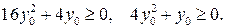
Следовательно, 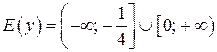 . При этом ни наибольшего, ни наименьшего значения функция не имеет. Значение
. При этом ни наибольшего, ни наименьшего значения функция не имеет. Значение 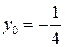 функция принимает при
функция принимает при 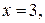 значение
значение 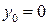 функция не принимает. Точка
функция не принимает. Точка 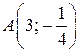 принадлежат графику функции
принадлежат графику функции 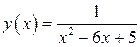 . Данная функция не ограничена ни сверху, ни снизу и, следовательно, не ограничена. На интервале
. Данная функция не ограничена ни сверху, ни снизу и, следовательно, не ограничена. На интервале 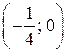 нет ни одной точки графика функции.
нет ни одной точки графика функции.
При 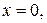
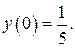
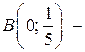 точка пересечения графика функции
точка пересечения графика функции 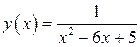 с осью
с осью 
Исследуем функцию 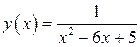 на четность. Область определения функции
на четность. Область определения функции 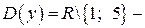 не симметричное относительно начала координат множество, следовательно,
не симметричное относительно начала координат множество, следовательно, 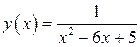 функция общего вида.
функция общего вида.
Функция 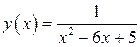 непериодическая.
непериодическая.
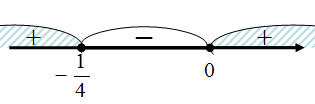
Определим промежутки знакопостоянства данной функции:
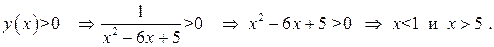 То есть
То есть 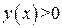 на
на 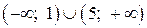 ,
, 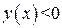 на
на 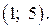 График данной функции лежит выше оси
График данной функции лежит выше оси 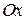 на
на 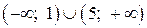 , ниже оси
, ниже оси 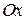 на
на 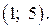
Определим промежутки монотонности функции 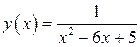 .
.
Пусть 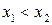 . Сравним
. Сравним 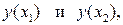 где
где 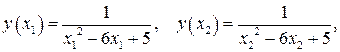 имеем
имеем
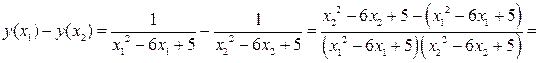
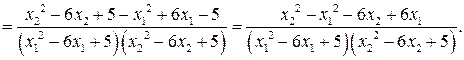
Установим знак выражения 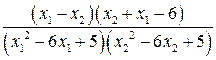 .
.
По условию 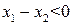 . Определим знак выражения
. Определим знак выражения 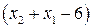 . Для этого заменим
. Для этого заменим 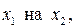 имеем:
имеем: 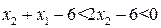
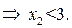
Выражение 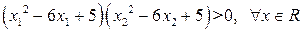 .
.
Следовательно, на 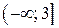 функция
функция 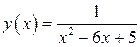 возрастает.
возрастает.
Аналогично, на 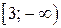 функция
функция 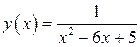 убывает.
убывает.
Эскиз графика функции 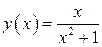 приведен на рисунке 89.
приведен на рисунке 89.
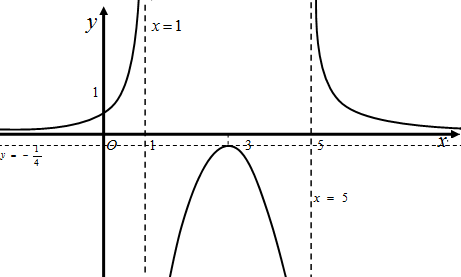
Рис. 89
Пример 4. Проведем исследование функции 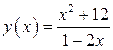 и построим эскиз ее графика.
и построим эскиз ее графика.
Решение. Определим область определения функции 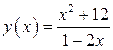 :
: 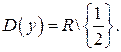
Найдем множество значений функции 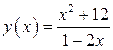 .
.
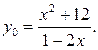 Если
Если 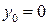 , то уравнение
, то уравнение 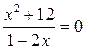 не имеет корней. Значит график функции не пересекает ось
не имеет корней. Значит график функции не пересекает ось  .
.
Пусть 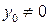 , тогда
, тогда 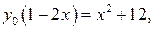
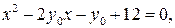
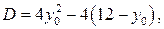
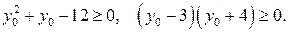
Следовательно, 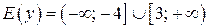 . При этом ни наибольшего, ни наименьшего значения функция не имеет. Значение
. При этом ни наибольшего, ни наименьшего значения функция не имеет. Значение 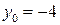 функция принимает при
функция принимает при 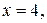 значение
значение 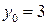 функция принимает при
функция принимает при 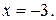 Точки
Точки 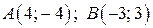 принадлежат графику функции
принадлежат графику функции 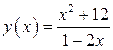 . Данная функция не ограничена ни сверху, ни снизу и, следовательно, не ограничена. На интервале
. Данная функция не ограничена ни сверху, ни снизу и, следовательно, не ограничена. На интервале 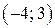 нет ни одной точки графика функции.
нет ни одной точки графика функции.
При 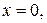
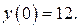
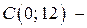 точка пересечения графика функции
точка пересечения графика функции 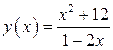 с осью
с осью 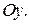
Исследуем функцию 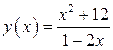 на четность. Область определения функции
на четность. Область определения функции 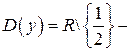 не симметричное относительно начала координат множество, следовательно,
не симметричное относительно начала координат множество, следовательно, 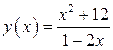 функция общего вида.
функция общего вида.
Функция 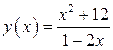 непериодическая.
непериодическая.
Определим промежутки знакопостоянства данной функции:
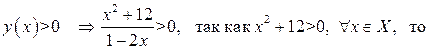
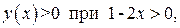
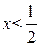 . То есть
. То есть 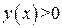 , при
, при 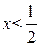 ;
; 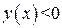 , при
, при 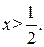 График данной функции лежит выше оси
График данной функции лежит выше оси  при
при 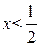 , ниже оси
, ниже оси 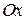 при
при 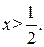
Определим промежутки монотонности функции 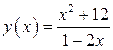 .
.
Пусть 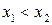 . Сравним
. Сравним 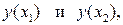 где
где 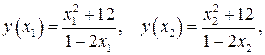 имеем
имеем
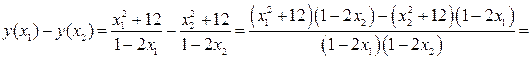
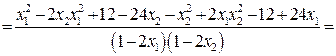
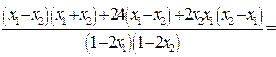
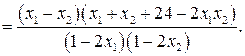
Установим знак выражения 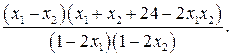 .
.
По условию 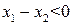 . Определим знак выражения
. Определим знак выражения 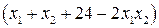 . Для этого заменим
. Для этого заменим 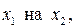 имеем:
имеем: 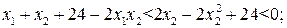
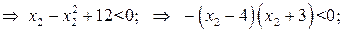

Определим знак выражения 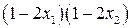 .
. 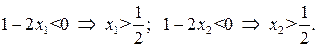
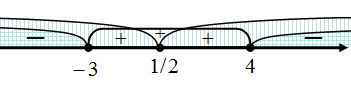
Следовательно, на 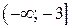 и на
и на 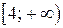
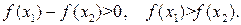 Таким образом, на
Таким образом, на 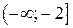 и на
и на 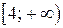 функция
функция 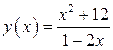 убывает.
убывает.
Аналогично, на 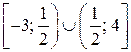 функция
функция 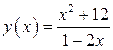 возрастает.
возрастает.
Следовательно, 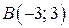 – точка минимума функции
– точка минимума функции 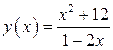 ;
; 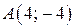 – точка максимума функции
– точка максимума функции 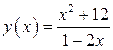 .
.
Эскиз графика функции 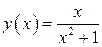 приведен на рисунке.
приведен на рисунке.
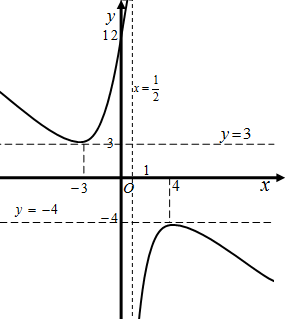
Рис. 90
 2015-04-23
2015-04-23 757
757







