Для расчета надежности широко используют структурные схемы, в том случае, когда возможно расчленение сложной системы на отдельные независимые элементы. В этих схемах каждый /-й элемент характеризуется вероятностью его безотказной работы р, в течение заданного периода времени и по этим значениям определяют вероятность безотказной работы P{t) всей системы. Такие расчеты обычно называются расчетом схемной надежности.
Наиболее характерен случай, когда отказ одного элемента выводит из строя всю систему, как это имеет место, например, при
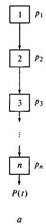
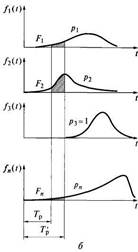
Рис. 4.2. Схема последовательного соединения элементов сложной системы: последовательное соединение элементов; б — вероятности безотказной работы элементов
а — после
последовательном соединении элементов (рис. 4.2, а). Так, если в приводе машины откажет любой из его элементов — электродвигатель, редуктор, муфты, механизмы управления, насос смазки, то весь привод перестанет функционировать. При этом отдельные элементы не обязательно должны быть соединены последовательно.
Вероятность безотказной работы такой системы равна произведению вероятностей безотказной работы элементов (по теореме умножения вероятностей независимых событий):
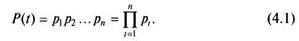
При одинаковой надежности элементов формула (4.1) примет вид

Сложные системы, состоящие из элементов высокой надежности, могут обладать низкой надежностью за счет наличия большого числа элементов.
Например, если узел состоит всего из 50 деталей, а вероятность безотказной работы каждой детали за выбранный промежуток времени составляет р, = 0,99, то вероятность безотказной работы узла будет P{t) = (0,99)50 = 0,55. Если же узел с аналогичной безотказностью элементов состоит из 400 деталей, то P(t) = (0,99)400 = 0,018, т. е. узел становится практически неработоспособным.
Для расчета надежности системы должен быть известен закон распределения сроков службы (наработки) для каждого элемента.
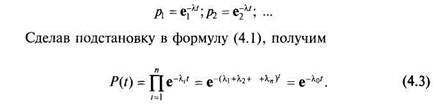 |
| Таким образом, вероятность безотказной работы сложной системы в этом случае также подчиняется экспоненциальному закону с параметром |
 |
При внезапных отказах часто применяют экспоненциальный закон, в котором параметром является интенсивность отказов X = = const, и вероятность безотказной работы элементов определяется как
Схема формирования значения вероятности безотказной работы для системы с последовательно соединенными элементами показана на рис. 4.2, б.
При изменении периода t = Тр (ресурса), в течение которого рассматривается работа системы, изменяется и значение р, для каждого элемента. Так, для изображенного на рис. 4.2, б случая при увеличении ресурса от Тр до Тр' вероятность отказа первого элемента возрастет в 2,5 раза, второй элемент станет практически неработоспособным (р2 = 0,5), а третий элемент по-прежнему не будет лимитировать значение P(t) для всей системы.
При анализе и расчете надежности элементов системы необходимо использование принципов системного подхода, когда данный механизм, двигатель, электронное устройство рассматриваются как составные части более сложной системы, когда оценивается влияние его надежности на все основные характеристики автомобиля и, в конечном итоге, на эффективность его функционирования.
• Количественно надежность системы зависит главным образом от трех факторов:
• - надежности элементов, входящих в состав автомобиля;
• характера соединения элементов;
• временных характеристик (времени работы элементов на данном режиме).
Только совместное рассмотрение всех перечисленных факторов и их влияния на другие характеристики установки позволит определить требования к надежности отдельных элементов, а также наиболее рациональные мероприятия, направленные на ее повышение.
Для повышения надежности сложных систем применяют метод резервирования, т.е. создают дополнительные средства и возможности для сохранения работоспособности системы при отказе одного или нескольких ее элементов. При резервировании ненадежных элементов после отказа основного элемента дублер выполняет его работу, и узел продолжает функционировать. Резервирование может значительно повысить надежность системы.
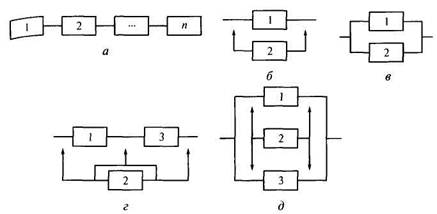
Рис. 4.3. Схемы соединения элементов в составе системы:
а — последовательное (основное) соединение элементов; б — резервирование замещением — ненагруженный резерв; в — параллельная работа элементов — нагруженный резерв; г — скользящий резерв с последовательной работой элементов 1 и 3; д — скользящий резерв с параллельной работой элементов 1 и 3
Для расчета надежности на основании принципиальной схемы составляется функциональная (структурная) схема установки, отражающая характер связей элементов в ее составе с точки зрения надежности осуществления рабочего процесса. При составлении функциональных схем используют обозначения, представленные на рис. 4.3. Рассмотрим кратко каждую из указанных на этом рисунке схем.
1. Последовательное (основное) соединение элементов (рис. 4.3, а). Отказ любого из элементов 1, 2,..., п приводит к отказу всей Последовательной системы. Указанная система содержит минимально необходимое для осуществления рабочего процесса число элементов. В случае отказа одного (любого) из элементов система не работает, отказавший элемент восстанавливается (ремонтируется или заменяется). В составе автомобиля во многих случаях последовательно соединены двигатель, коробка передач, карданный вал, редуктор, колеса. Последовательно соединены и многие вспомогательные механизмы. Рассматриваемая схема является наиболее распространенной, расчеты характеристик ее надежности делаются наиболее часто.
2. Резервирование замещением — ненагруженный резерв (рис. 4.3, б). В случае отказа основного элемента 1 включается резервный элемент 2. Отказавший элемент восстанавливается и ставится в резерв. Если работающий элемент откажет раньше, чем закончитсявосстановление отказавшего, наступает отказ системы и восстанавливаются оба элемента. По такой схеме резервируют вспомогательные механизмы: топливные, масляные и другие насосы.
3. Параллельная работа элементов — нагруженный резерв (рис. 4.3, в). Элементы 1 и 2 работают параллельно на один потребитель.
4. В случае отказа любого из них второй продолжает работу, отказавший элемент восстанавливается и включается в работу. Если оставшийся исправным элемент откажет раньше, чем восстановится отказавший, наступает отказ системы и восстанавливаются оба элемента. Иногда на один потребитель работает более двух элементов. По такой схеме резервируют, например, электрогенераторы и элементы сложной системы охлаждения.
5. Скользящий резерв (рис. 4.3, г, д):
• элементы 1 и 3 (см. рис. 4.3, г) работают последовательно. При отказе любого из них вместо него включается резервный элемент 2. Отказавший элемент восстанавливается и ставится в резерв. Если один из работающих элементов откажет раньше, чем восстановится отказавший, наступает отказ системы и восстанавливаются оба отказавших элемента. Эта схема используется в конструкциях автомобильной техники реже, чем рассмотренные ранее схемы;
• элементы 1 и 3 (см. рис. 4.3, д) работают параллельно на один потребитель. При отказе любого из них включается резервный элемент 2. Отказавший элемент восстанавливается и ставится в резерв. Если один из работающих элементов откажет раньше, чем восстановится отказавший, восстанавливаются оба элемента. По такой схеме резервируют в ряде случаев элементы тормозных систем.
Указанные схемы соединения элементов в составе системы не являются единственно возможными, но на практике используются наиболее часто.
Зная функциональную схему установки и характеристики надежности входящих в ее состав элементов, можно оценить надежность различных схем соединения элементов, а затем и установки в целом.
Во время эксплуатации автомобиль работает в режимах, разли-чающихся продолжительностью, номенклатурой включенных элементов и нагрузкой на них, что обусловливает различную надежность обеспечения режимов. Поэтому функциональные схемы целесообразно составлять для каждого режима. Однако часто достаточно выполнить расчет надежности для наиболее напряженного режима работы автомобиля.
Рассмотрим методы расчета характеристик надежности представленных на рис. 4.3 схем соединения элементов и начнем с определения надежности последовательного соединения элементов.
Допустим, имеются два последовательно соединенных элемента (см. рис. 4.3, а), например, двигатель и коробка передач. Присвоим этим элементам номера 1 и 2 соответственно.
Безотказная работа последовательной системы за время t есть событие, заключающееся в исправной работе за указанное время элементов 1 и 2. Тогда в предположении независимости отказов элементов (такое предположение, как правило, делается в теории надежности) вероятность безотказной работы системы можно записать в виде

где P\(J), P2(t) — вероятности безотказной работы элементов 1 и 2 соответственно.
Зная P{i) и используя приведенные ранее взаимосвязи между показателями надежности, будем иметь:
вероятность отказа
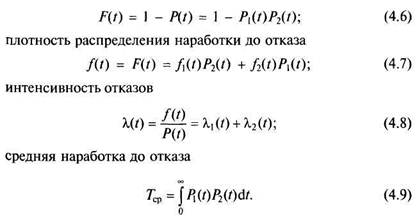
Зависимости (4.5) —(4.9) справедливы для любых законов распределения наработки до отказа элементов и, к тому же, легко Могут быть обобщены на случай последовательной системы из п элементов. Подставляя в них, в частности, соответствующие выражения для экспоненциального закона (именно этот закон чаще других применяется в расчетах надежности элементов автомобиля), можно получить
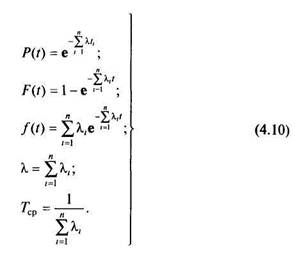
Эти зависимости свидетельствуют о том, что если наработка до отказа каждого элемента распределена экспоненциально, то наработка до отказа последовательной системы также распределена экспоненциально.
Рассматривая зависимости (4.10), можно сделать вывод о том, что при достаточно большом числе элементов я надежность последовательной системы намного меньше надежности любого из ее элементов. Поэтому одним из эффективных средств повышения надежности последовательной системы является уменьшение числа п образующих ее элементов. Однако уменьшение часто связано с изменением других характеристик автомобиля. Так, исключение из состава автомобиля подогревателей охлаждающей жидкости уменьшает число отказов, однако при этом ухудшаются экономические показатели двигателя. При использовании трехступенчатой коробки передач для передачи крутящего момента на колеса автомобиля увеличивается надежность (при прочих равных условиях) по сравнению с другими типами коробок передач (четырех-, пятиступенчатой и автоматической коробкой передач, где больше число элементов), однако ухудшаются скоростные и экономические характеристики автомобиля.
Таким образом, при исследовании и проектировании технических систем показатели надежности необходимо рассматривать во взаимосвязи с другими характеристиками для принятия оптимальных решений.
Найдем теперь комплексные показатели надежности, учитывающие как безотказность, так и ремонтопригодность системы. 0усть, как и ранее, система состоит из двух последовательно сочиненных элементов. Будем предполагать, что время работы до оТказа и продолжительность восстановления элементов распределены по показательному закону с параметрами \и Х2, \i\, \i2 соответственно. В произвольный момент времени система может находиться в двух состояниях: работоспособном или неработоспособном. Обозначим вероятности нахождения в этих состояниях через p(t) и ДО- Система может оказаться в состоянии отказа вследствие отказа либо первого, либо второго элемента. Вероятности этих событий обозначим соответственно через f\(t),f2(t). Поскольку при экспоненциальном распределении поток отказов является простейшим и, следовательно, ординарным, то здесь и далее можно пренебречь вероятностью одновременного отказа двух элементов. Тогда ясно, что/(0 =/i(0 +/г(0- Здесь и далее в этой главе вероятность нахождения восстанавливаемой системы или элемента в работоспособном состоянии (функция готовности) в момент / вероятности противоположного события обозначим строчными буквами р и/соответственно в отличие от прописных букв Р и F, означающих вероятности безотказной работы и отказа в промежутке (О, О-
Рассмотрим теперь момент времени (/ + At). Работоспособное состояние системы в этот момент есть событие, являющееся суммой трех несовместных событий:
• в момент t система работоспособна, и за время At ни один из элементов не отказал;
• в момент / система находилась в состоянии отказа вследствие неисправности элемента 1, но за время At этот элемент был восстановлен;
• в момент / система находилась в состоянии отказа вследствие неисправности элемента 2, но за время At этот элемент был восстановлен.
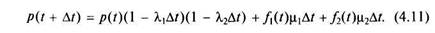
| Перенеся p(t) в левую часть, разделив обе части на At и перейдя к пределу при At —> О, будем иметь |
Учитывая, что с точностью до бесконечно малых высшего порядка по сравнению с At вероятности отказов элементов на промежутке At равны соответственно Л^Д/, "K2At, вероятности восстановления в течение At определяются произведениями \i\At, \i2At, a вероятности противоположных событий равны соответственно 1 - XiAt, 1 - X2At, I - ц,Л? и 1 - \i2At, функция готовности, т.е. вероятность p(t + At) работоспособного состояния системы в момент (/ + At) можно записать в виде
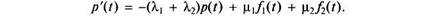
Событие, состоящее в том, что в момент t + At система находится в состоянии отказа вследствие неисправности элемента 1, является суммой двух несовместных событий:
• система исправна в момент t, но за время At элемент 1 отказал;
• система находится в рассматриваемом состоянии в момент t, но за время At восстановление этого элемента не закончено.
Таким образом, вероятность f\{t){t + At) можно представить в виде
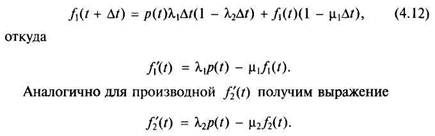
Учитывая, что p{t) + /,(/) + f2(t) = 1, для определения вероятностей p{t), /i(/), fiit) будем иметь следующую систему уравнений:
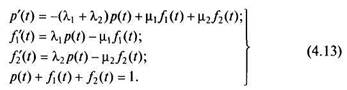
Разрешив эту систему, получим искомые вероятности как функции времени. Эти вероятности достаточно быстро (через 200... 500 ч) сходятся к своим предельным, не зависящим от времени значениям. При этом, естественно, производные в системе (4.13) становятся равными нулю. Поскольку надежность работы систем автомобиля и их отдельных элементов рассчитывается обычно для более продолжительного времени, наибольший интерес представляют именно эти предельные величины. Обозначим их, соответственно, через р, f\ и /2. Поскольку эти вероятности от времени не зависят, то, преобразовав систему (4.13), получим
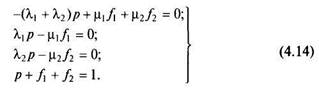
решая систему относительно искомых вероятностей, найдем
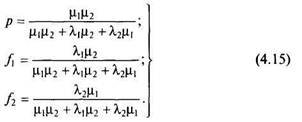
Теперь можно записать и вероятность того, что система находится в неисправном состоянии:
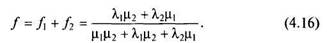
Числитель и знаменатель первого равенства из системы (4.15) и выражения (4.16) разделим на \iu \i2. Введя обозначения ух = = Л-i/jj,! и Y2 = ^г/М-2 выражения для р и/можно записать в виде
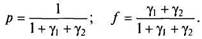
| Обобщая этот результат на систему, имеющую в своем составе и последовательно соединенных элементов, найдем |

Очевидно, что вероятность р представляет собой стационарное значение коэффициента готовности системы.
Найдем теперь интенсивность восстановления и, следовательно, среднее время восстановления последовательной системы. Для этого воспользуемся тем, что, как было указано, безотказность системы эквивалентна безотказности одного элемента с интен-
я
сивностью отказов Х = ^Х,. Тогда выражение для предельного
значения коэффициента готовности этого элемента можно записать следующим образом:

где д — искомая интенсивность восстановления последовательной системы.
Как и ранее, рассмотрение начнем со случая двух последовательно соединенных элементов. Если приравнять первое из равенств системы (4.15) и выражение (4.18)
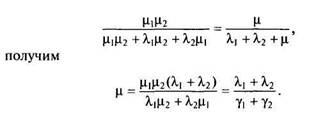
Обобщение на случай п последовательно соединенных элементов имеет вид

Зная интенсивность восстановления последовательной системы, можно найти и среднее время восстановления
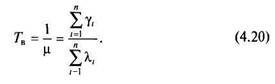
Пример 4.1. Рассмотрим три элемента технической системы (автомобиля): двигатель, коробку передач и карданный вал. Заданы следующие значения интенсивности отказов X и восстановлений ц этих элементов:

Теперь, используя приведенные ранее зависимости, можно установить и другие показатели надежности, например:

Рассмотрим надежность схемы с непогруженным резервом для частного случая резервирования — дублирования. Пример компоновки такой схемы показан на рис. 4.3, б.
В произвольный момент времени / система может находиться в одном из трех состояний:
• исправном (один из элементов работает, другой — в холодном резерве);
• один из элементов находится в состоянии отказа, другой исправен (исправный элемент работает, отказавший — восстанавливается);
• оба элемента находятся в состоянии отказа и, следовательно, восстанавливаются.
Определим вначале методы расчета характеристик безотказности, т.е. рассмотрим случай, когда восстановление элементов не учитывается. Вероятности перечисленных состояний обозначим через P(t), F{(t) и F2(t) соответственно.
Вероятность нахождения системы в момент / в интервале (0, t) в исправном состоянии есть вероятность безотказной работы элемента / за время /, т.е. P(t) = P\{t).
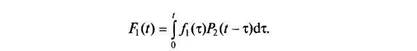
| Вероятность F2(t) есть вероятность отказа элемента 1 в момент T(t < t) и отказа элемента 2 в момент 0(т < 8 < /), следовательно, |
Вероятность Fx{t) есть вероятность отказа элемента 1 в момент т, (т < t) и исправной работы элемента 2 в интервале (т, t). Таким образом:
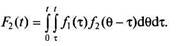
Подставляя в эти зависимости вместо J[t) и P(t) их значения для показательного распределения времени работы до отказа, найдем

Если основной и резервный элементы имеют одинаковую надежность, т.е. если X = X, = Х2, то, раскрывая неопределенность в системе (4.21), окончательно получаем
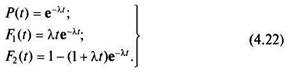
Зная указанные величины, нетрудно найти и другие характеристики надежности. Отметим только, что средняя наработка системы до отказа (время до отказа обоих элементов системы) равна сумме средних наработок до отказа элементов, т.е.
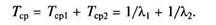
Рассмотрим теперь влияние восстановления для случая X = А,, = = Х2 и Ц! = ц,2 = Ц- Обозначим вероятности нахождения системы в произвольный момент времени t в указанных ранее состояниях с учетом восстановления элементов после отказа через p(t), f{(t) и fi{t). Уравнения для определения этих вероятностей, составленные для равнонадежных элементов 1 и 2, как и в случае последовательного соединения, имеют вид
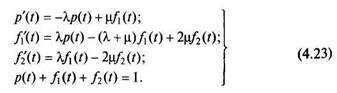
Систему алгебраических уравнений для определения предельных значений искомых вероятностей получим в виде
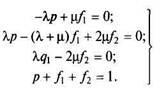
Решая эту систему, найдем

Ранее указаны расчетные зависимости для показателей надежности системы с ненагруженным резервом. Данные (или аналогичные им) показатели рассчитывались ранее для нерезервированного элемента и для последовательной системы. Однако наличие резервного элемента не только количественно изменяет характеристики надежности, но и оказывает качественное влияние. Так, для резервированных систем особое значение приобретают показатели надежности, которые не могут быть рассчитаны в схемах без резерва. К их числу относится вероятность безотказной работы системы с учетом восстановления элементов. Обозначим
ее через P(t). Отказ обоих элементов означает отказ дублированной системы. При отказе одного элемента второй продолжает работу, отказавший элемент восстанавливается. Однако возможен случай, когда работающий элемент откажет раньше, чем восстановится отказавший. Это приведет к отказу системы. Величина P(t) представляет собой вероятность события, состоящего в том, что за время / указанной ситуации не произойдет. Для нахождения этой вероятности будем считать состояние отказа обоих элементов поглощающим состоянием системы. Тогда искомая вероятность P{t) = 1 - /(/), где вероятность отказа системы, обозначенная как /(/), с учетом восстановления элементов определится из уравнений, описывающих работу дублированной системы с учетом поглощающего состояния. Эти уравнения могут быть получены из сИстемы (4.23), если исключить из нее члены; определяющие вы ход из поглощающего состояния, т. е. члены, содержащие множитель 2ц. Таким образом, будем иметь
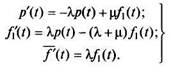
Решая эту систему, найдем вероятность f'(t) и, следовательно, P(t). Теперь можно определить и среднюю наработку систе-
оо
мы до отказа с учетом восстановления элементов Гср = J P(t)dt.
Выполнив все указанные вычисления, окончательно получим
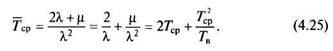
Выражение (4.25) показывает, что величина Тер состоит из двух слагаемых. Первое слагаемое 2 Гср определяет влияние резервирования без учета восстановления, второе слагаемое Tlp/TB характеризует именно влияние восстановления. Представляет интерес сравнение значений этих двух членов.
Пусть, например, среднее время работы до отказа элементов Гср = 5 000 ч, а средняя продолжительность восстановления Тв = 50 ч. Тогда среднее время работы до отказа с учетом восстановления
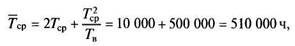
т.е. эффект восстановления вносит определяющий вклад в значение величины Тер. Отсюда очевидна особая актуальность обеспечения ремонтопригодности элементов, входящих в состав резервированных систем. Именно возможность восстановления отказавшего элемента резко увеличивает эффект резервирования.
Пример 4.2. Циркуляционный насос смазочной системы двигателя резервируется по схеме замещения. Интенсивности отказов и восстановлений каждого насоса соответственно X = 2 ■ Кг4 1/ч, ц = 2 • 10"' 1/ч.
Определить характеристики надежности резервированной системы.
Решение. В соответствии с зависимостями (4.22) и (4.24):
вероятность безотказной работы основного элемента
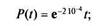

| вероятность отказа одного элемента |
Рассмотрим надежность параллельной работы элементов, показанных на рис. 4.3, в.
Такая схема часто встречается на практике, когда равнонадеж-ные элементы 1 и 2 работают на один потребитель с некоторой нагрузкой N.
При отказе одного из них другой продолжает работу с нагрузкой N' (интенсивность отказов А,'), отказавший элемент восстанавливается с интенсивностью ц. Если в состоянии отказа находятся оба элемента, они восстанавливаются с интенсивностью 2\i.
В произвольный момент времени система может находиться в одном из трех состояний:
• исправном (работают оба элемента);
• один из элементов отказал и восстанавливается, другой продолжает работу;
• оба элемента находятся в состоянии отказа и восстанавливается (отказ системы).
Как и ранее, вначале рассмотрим показатели безотказности. Вероятности указанных состояний обозначим соответственно через ДО, /\(0 и F2(t).
Вероятность нахождения системы в первом из перечисленных состояний есть вероятность события, являющегося произведением двух событий, заключающихся в исправной работе элементов 1 и 2 за время t, т.е. P{t) = Pl(t)P2(t).
Вероятность Fi(t) есть вероятность события, состоящего в отказе одного из элементов в момент т(т < t) и исправной работе другого элемента в промежутке (0, t):
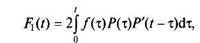
где P\t - т) — вероятность безотказной работы элемента, работающего в течение времени (/ - т) с нагрузкой N'.
Вероятность F2{t) определяется как вероятность события, заключающегося в отказе одного из элементов в момент т < t и другого — в момент Э(х < 9 < t)
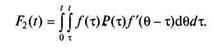
Для показательного распределения времени работы до отказа элементов будем иметь
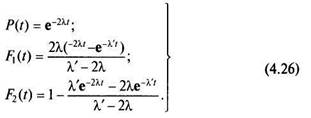
Если изменения нагрузки после отказа одного из элементов не происходит, т.е. если X' = X, то, раскрывая неопределенность в системе (4.26), получаем
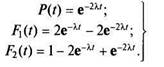
Зная эти вероятности, можно найти и другие показатели безотказности. Отметим только, что средняя наработка системы до
0тказа обоих элементов, полученная интегрированием вероятности 1 - Fi(t), равна Гср = 1/(2Х) + 1/А'.
Если перераспределения нагрузки не происходит, то Тср = 3/(2А,).
Рассмотрим теперь показатели надежности системы с учетом восстановления элементов. Обозначим вероятности нахождения системы в указанных ранее состояниях в произвольный момент времени (соответственно через p{t), /,(/) nf2(t)).
Уравнения, описывающие работу системы, т.е. уравнения для определения этих вероятностей, будут иметь вид
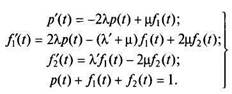
Алгебраическую систему уравнений для определения финальных значений искомых вероятностей запишем в виде
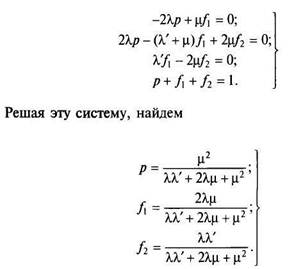
Найдем теперь среднюю наработку системы до отказа с учетом восстановления элементов. Уравнения, описывающие работу системы при наличии поглощающего состояния, имеют вид
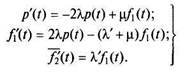
Решая эту систему, найдем p{t) = \-f2(t) и, наконец, среднюю наработку до отказа системы с учетом восстановления элементов.
Пример 4.3. Элементы смазочной системы двигателя работают параллельно. Интенсивность отказов элементов X = 3 • 10^8 1/ч. Интенсивность восстановления ц = 2,5 • 10~2 1/ч.
Определить показатели надежности резервированной системы в предположении, что при отказе одного из маслоохладителей нагрузка другого не меняется.
Решение. Воспользуемся приведенными ранее зависимостями:
вероятность безотказной работы

рассмотрим надежность скользящего резерва, схема которого представлена на Рис- 4.3, г.
В произвольный момент времени система может находиться в одном из следующих состояний:
. исправном (работают два элемента, третий — в резерве);
* отказавший элемент восстанавливается, два оставшихся продолжают работу;
• два отказавших элемента восстанавливаются, третий исправен, но не работает (отказ системы).
Вероятности указанных состояний обозначим соответственно через I\t), Fx{t) и F2(t).
В промежутке (0, i) работают элементы 1 и 3, т.е.
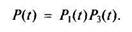
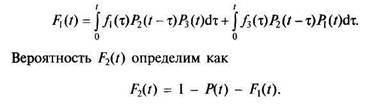
Для показательного распределения времени работы до отказа и равнонадежных элементов будем иметь
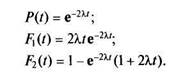
Вероятность Fx(t) есть вероятность события, состоящего в отказе элемента 1 или 3 в момент т(т < t) и исправной работе оставшегося элемента и резервного до момента V.
С помощью этих вероятностей можно найти и другие показатели надежности. Приведем лишь формулу для средней наработки До отказа: Гср = 1 Д. Таким образом, с точки зрения среднего времени работы до отказа рассматриваемая схема резервирования аналогична схеме с одним нерезервированным элементом.
Рассмотрим теперь показатели надежности с учетом восстановления элементов.
Обозначим вероятности нахождения системы в указанных ранее состояниях соответственно через p(t), fx(t) и/2(0- Пусть элементы 1, 2 и 3 равнонадежны, т.е.?ц = Х2 = ^з = ^ и имеют одинаковую интенсивность восстановления \i. Тогда уравнения, описывающие работу системы, можно записать в виде
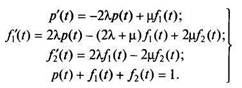
Решая эту систему, получаем
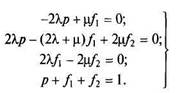
Решая эту систему, найдем искомые вероятности как функции времени. Однако, как и ранее, нас интересуют предельные, не зависящие от времени значения этих вероятностей. Их найдем из следующей системы алгебраических уравнений:
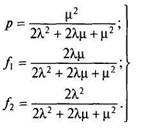
Аналогично изложенному ранее можно найти среднюю наработку до отказа системы с учетом восстановления элементов. Для этого следует составить уравнения, описывающие работу резервированной системы при наличии поглощающего состояния. Не будем приводить эту систему уравнений, поскольку ее можно легко получить из приведенных ранее зависимостей путем исключения из них членов, содержащих множитель 2ц.. Выполняем операции, необходимые для подсчета Тср (они аналогичны рассмотренным ранее):
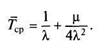
Пример 4.4. Элементы системы охлаждения двигателя соединены по схеме скользящего резерва. Интенсивности отказов и восстановления элементов соответственно равны X = 1 • 10~5 1/ч; ц = 1 • 10~2 1/ч.
Определить показатели надежности резервированной системы.
Решение. Воспользовавшись полученными формулами, запишем: вероятность безотказной работы двух основных насосов

Рассмотрим схему, представленную ранее на рис. 4.3, д. Пусть в произвольный момент времени t резервированная система может находиться в одном из следующих состояний:
• исправном (элементы 1 и 3 работают, элемент 2 в резерве);
• один из элементов отказал и восстанавливается, оставшийся
исправным и резервный работают;
• два отказавших элемента восстанавливаются, оставшийся исправным элемент продолжает работу с некоторой нагрузкой N', отличающейся от нагрузки при двух работающих элементах;
• три отказавших элемента восстанавливаются (отказ системы).
Найдем вначале показатели безотказности. Вероятности указанных ранее событий в промежутке (0, /) обозначим соответственно через P{t), Fi(t), F2(t) и F3(t). Далее будем предполагать элементы 1, 2 и 3 равнонадежными. Исправная работа системы в промежутке (0, /) есть событие, состоящее в безотказной работе элементов 1 и 3, т.е.
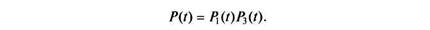
Вероятность F{(t) есть вероятность события, состоящего в отказе элемента 1 или 3 в момент х(т < /) и исправной работе оставшегося рабочего и резервного элементов до момента /:
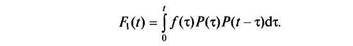
Вероятность F2(t) определится из условия отказа одного из элементов в момент х, отказа второго рабочего или резервного элемента в момент 9(х < 9 < /) и исправной работе оставшегося элемента до момента V.

где X, X' — интенсивность отказов элементов при нагрузке Nn N' соответственно.
Если при отказе двух элементов нагрузка на оставшийся не меняется, т.е. если N= № и X = X', то указанные ранее зависимости будут иметь вид
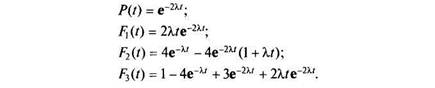
Средняя наработка системы до отказа, полученная интегрированием вероятности 1 - F3(t),
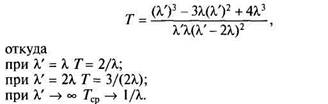
Таким образом, если при отказе двух элементов режим работы третьего не меняется (к = X'), то относительно величины Т рассматриваемая схема резервирования эквивалентна схеме резервирования замещением (случай равнонадежных элементов). Если режим работы меняется так, что при нагрузке интенсивность отказов удваивается, данная схема резервирования эквивалентна схеме постоянно включенного резерва (случай X = X'). Наконец, если при нагрузке № интенсивность отказов весьма велика, то Т равно среднему времени работы до отказа нерезервированного элемента. Эти выводы свидетельствуют о возможности сравнения различных схем резервирования элементов систем автомобиля и выбора оптимальной схемы с учетом данных о стоимости и мас-согабаритных характеристик различных схем.
Рассмотрим теперь показатели надежности, учитывающие восстановление элементов после отказа. Для этого случая вероятности нахождения системы в произвольный момент времени t в одном из перечисленных ранее состояний обозначим через p{t), fx{t), flit) и fi(t) соответственно.
Уравнения, описывающие работу резервированной системы с Учетом восстановления, имеют вид
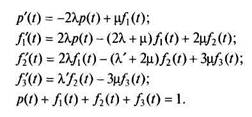
Для предельных значений искомых вероятностей имеем следующую систему алгебраических уравнений:

Пример 4.5. Элементы системы работают по схеме скользящего резерва (см. рис. 4.3, д). Значения интенсивности отказов и восстановлений соответственно Х = 2- 10"4 1/ч, ц = 2,5-10~2 1/ч.
Определить основные показатели надежности в предположении, что при отказе двух генераторов нагрузка оставшегося исправным не изменяется (X' = X).
Решение. Воспользовавшись полученными формулами, запишем:
вероятность исправной работы
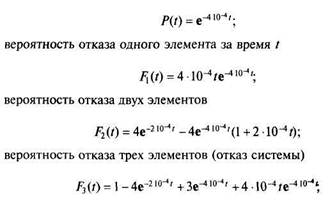

 2015-04-23
2015-04-23 4756
4756