Решение. Для 99%-ного интервала обратная функция Лапласа F’=2,58s`

s_`X = Ö(D*/n)= 0,005. Т.о. 95%-ный интервал:

I_95% =(t_ср-1,96s_{`X</sub>; t<sub>ср</sub>+1,96s<sub>`X})=(1,73 ± 1,96*0,005)=[1,72; 1,74].

Для 99%-ного интервала обратная функция Лапласа F’=2,58s_`X:

I_99%=(t_ср-2,58s_{`X</sub>;t<sub>ср</sub>+2,58s<sub>`X})=(1,73 ± 2,58*0,005)=(1,717;1,743).

Важно правильно интерпретировать вероятностное выражение, стоящее в доверительном интервале. Утверждение P(b₁ £ b £ b₂)= p означает, что для данного интервала, выбранного из совокупности интервалов, вероятность содержать значение b равна р. Т.е если рассматривать большое число выборок и каждый раз вычислять интервалы (b₁, b₂), то приближенно 100% из них содержали бы значение b, а остальные - не содержали бы.

Точное вычисление доверительного интервала

В выборках малого (n<200) объема[1] величина выборочной дисперсии, а следовательно, и с.к.о. может быть в значительной степени подвержено влиянию случайностей выборки. Для уменьшения этого влияния при расчете доверительных интервалов для параметров малых выборок пользуются так называемым отношением Стьюдента (фактическое нормированное отношение):

(m_x - 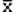) l

t = ¾¾¾¾¾ = ¾¾, (2.30)

s_{`X</sub> s<sub>`X}

s_выб.

где s_`X = ¾¾¾.

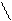
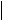
n-1

Доказано, что при нормальном распределении генеральной совокупности X случайная величина t подчиняется так называемому «Закону распределения Стьюдента» (В.С.Госсета), плотность которого равна:

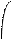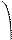_{Г{(k+1)/2} t}^{2 -(k+1)/2}

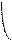
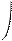
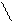
s(t,k)= ¾¾¾¾¾¾¾ 1+ ¾¾

Г{k/2} p k k, (2.31)

_¥

где Г{x} - известная гамма-функция: Г(x)= ò u^x-1e^-udu,

⁰

k=n-1 - число степеней свободы.

Вероятность того, что ошибка выборки l будет не больше заданной величины ts_`X, определяется интегральной функцией распределения:

_t

S(t,k)= ò s(t,k)dt. (2.32)

^-¥

Эта функция приводится в литературе в виде таблиц. Распределение, определяемое выражениями (2.31) и (2.32), возникает только в том случае, если выборка берется из генеральной совокупности с нормальным распределением признака. Для k>30 кривая S(t,k) близка к нормальному распределению величины t. С уменьшением k t-распреде-ление Стьюдента все более отклоняется от нормального. Поэтому для точного определения границ доверительного интервала в случае малых выборок из нормальной совокупности поступают следующим образом:

а) выбирают t_p такое, что P(|t|<t_p)=p (из таблиц t-распределения

Стьюдента);

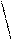D^**

б) раcсчитывают величину интервала: l = t_p ¾¾.

n

в) рассчитывают границы доверительного интервала:

I_p=(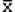 - l, 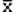+ l), (2.33)

где 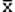- среднее выборочное.

В этом случае интервал I_p с вероятностью p накроет значение математического ожидания m_x генеральной совокупности.

Пример 2.13. На основании рейсовых отчетов капитанов выписана статистка загрузки Q лесовозов 5-тысячников и продолжительности T по 20-ти рейсам (табл. 2.9). Найти оценки математических ожиданий `Q и`T и построить доверительные интервалы I_p(Q) и I_p(T) с вероятностью p = 0,8.

Таблица 2.13

No,No рейсов
Загрузка Q, т
Продолжит. Т,сут

Табл. 2.13(продолжение)

No,No рейсов
Загрузка Q, т
Продолжит. Т,сут