Статистическое оценивание результатов эксперимента

Любая статистика, вычисленная по результатам выборки, сама является случайной величиной. Представляет интерес установление связи между выборочным распределением статистики и распределением совокупности, из которой производилась выборка - см. рис.2.8.

Например, выборочное среднее 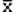может служить оценкой математического ожидания m_x. Но такой оценкой может быть и медиана 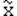. Спрашивается, какая из этих оценок величины m_x будет лучше? Можно ли найти другую выборочную статистику, в некотором смысле лучшую, чем

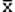и 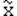? Решение этих вопросов составляет основу теории статистического оценивания. Эта теория дает два метода оценивания результатов эксперимента: точечное и интервальное оценивание.

Точечное оценивание

При точечном оценивании выборочная статистика, применяемая для оценки соответствующего параметра генеральной совокупности, называется точечной оценкой. Примеры точечных оценок:

n 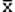может служить оценкой для m_x;

n 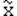может служить оценкой для m_x;

n D^* (дисперсия выборки) может служить оценкой для D (дисперсия генеральной совокупности).

Точечные оценки обладают следующими свойствами.

1) Несмещенность. Пусть b - некоторый параметр совокупности, а выборочная статистика b=f(x₁,...,x_n) - оценка этого параметра. Статистика b имеет свое выборочное распределение, характеризующееся средним M[b] и с.к.о. s^*[b].

Если M[b]=b, то b называется несмещенной оценкой b. В противном случае - смещенной.

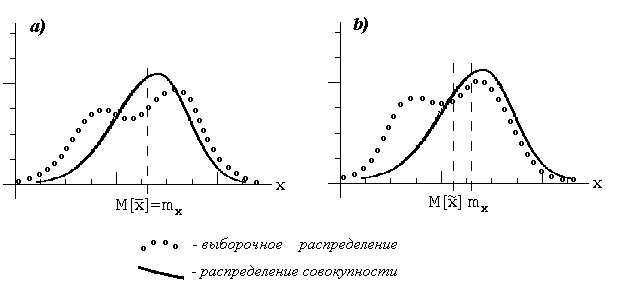Рис 2.9. Условие несмещенности (a) и смещенности (b) оценки

математического ожидания

Несмещенность - очень важное свойство, обладание которым желательно для любой оценки. Оно означает, что если пользоваться несмещенной оценкой, то в одних случаях может случиться, что мы завышаем искомый параметр совокупности, в других - занижаем, но в среднем - попадаем в цель.

Примеры:

- несмещенная оценка m_x (в теории статистического оценивания доказывается, что для любого распределения M[ ]=m_x);

- несмещённая оценка, если распределение совокупности симметрично;

S(x_i- )²

_n

D^* = ¾¾¾¾¾¾ - смещенная оценка дисперсии, поскольку:

N

n-1

M[D*]= ¾¾ D;

n

S(x_i- 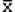)²

_n

D^** = ¾¾¾¾¾¾ - несмещенная оценка дисперсии;

n-1

S(x_i- 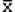)²

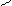_n

s^** = ¾¾¾¾¾¾ - смещенная оценка s.

n-1

Три последних примера наиболее заметны для малых выборок, т.е. таких, объем которых n < 30.

2) Эффективность. Если b₁ и b₂ - две несмещённые оценки параметра b и D[b₁]<D[b₂], то b₁ - более эффективная оценка, чем b₂ (т.е. более эффективна та, которая имеет меньшую дисперсию).

Оценка с наименьшей дисперсией называется наилучшей.

Пример:

s² p s²

D[ 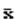]= ¾, D[ 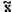]= ¾ × ¾, поэтому 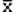- более эффективная

n 2 n

оценка математического ожидания m_x, чем .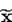

3) Состоятельность. Если выборочная статистика представляет собой несмещенную оценку параметра совокупности и D[b]®0 при n® ¥, то b называется состоятельной оценкой b.

Примеры:

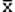- состоятельная оценка величины m_x, т.к. при n® ¥: s²® 0;

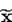- состоятельная оценка для нормального распределения совокупности (т.к. для него она несмещенная);

D* - состоятельная (но смещенная) оценка D.

Интервальное оценивание

Если производится на глаз оценка возраста человека, то можно сказать двояко, либо: «Ему 35 лет», либо «Ему от 32 до 38 лет» (вариант: «между 30 и 40»).

В первом случае — точечное оценивание, во втором — интервальное, причем в последнем можно определить и меру уверенности в правильности ответа («мне кажется», «я уверен», «ставлю... против...» и т.п.). Очевидно, что чем больше длина интервала, тем больше уверенности в том, что оцениваемая величина будет принадлежать этому интервалу. Этот пример иллюстрирует идею, лежащую в основе оценивания с помощью доверительных интервалов.

Пусть [2] для параметра b получена из опыта несмещенная оценка b. Задачей интервального оценивания является измерение возможной при этом ошибки. С этой целью назначается достаточно большая вероятность p (например, p = 0,9, 0,95 или 0,99), такая, что событие с этой вероятностью можно считать практически достоверным, и отыскивается такое значение l, для которого:

P(|b - b|< l)= p. (2.28)

Тогда диапазон практически возможных значений ошибки, возникающей при замене b на b, будет ± l. Большие по абсолютной величине ошибки будут появляться только с малой вероятностью q=1- p.

Равенство (2.28) означает, что с вероятностью p неизвестное значение параметра b попадает в интервал:

I_p =(b- l; b+ l). (2.29)

Особенность интервала, описываемого формулой (2.29), состоит в том, что его центр b и длина 2 l случайны (т.к. оценка b и значение l вычисляются по опытным данным), в то время как оцениваемое значение параметра b не случайно. Поэтому в данном случае вероятность p истолковывается не как вероятность «попадания» точки b в интервал, а как вероятность того, что случайный интервал I_p накроет точку b (см. рис. 2.10).

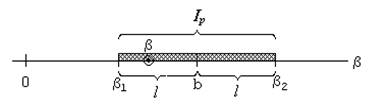
Рис. 2.10. Доверительный интервал

Вероятность p принято называть доверительной вероятностью, а интервал I_p - доверительным интервалом. Границы этого интервала: b₁=b- l и b₂=b+ l называются доверительными границами.

Теория статистического оценивания располагает двумя способами вычисления границ доверительных интервалов - приближенным и точным. Условия их применения различны.

Приближенное вычисление доверительного интервала

Центральная предельная теорема доказывает, что большинство выборочных статистик на практике имеют нормальное или приближенно нормальное распределение, причем:

s^*

s_`X = ¾¾,

n

где s^* - с.к.о. выборки объемом n,

s_`X - с.к.о. средневыборочного.

Это позволяет с помощью обратной функции Лапласа приближенно находить величину интервала (b-l, b+l), в котором будет лежать неизвестное значение b с заданной вероятностью (см. рис.2.11).

Например, для вероятности, равной 0.95 из таблицы F-распре-деления находим коэффициент доверия:

t = l /s_`X = 1.96

(для сравнения: если l = 2s, вероятность попадания в интервал p=0,954).

Следовательно, вероятность того, что значение b, определенное по выборке, лежит в интервале: (b-1,96s_{`X</sub>; b+1,96s<sub>`X}), равна 0,95.

Пример 2.12. Случайная выборка измерения времени обработки судна-контейнеровоза на специализированном причале для 100 судов дала результаты: t_ср=1,73 сут., D*=0,00245. Найти 95%-ный и 99%-ные доверительные границы для среднего совокупности, т.е. на бесконечное число обработок.