Метод симметричных составляющих относится к специальным методам расчета трехфазных цепей и широко применяется для анализа несимметричных режимов их работы, в том числе с нестатической нагрузкой. В основе метода лежит представление несимметричной трехфазной системы переменных (ЭДС, токов, напряжений и т.п.) в виде суммы трех симметричных систем, которые называют симметричными составляющими. Различают симметричные составляющие прямой, обратной и нулевой последовательностей, которые различаются порядком чередования фаз.
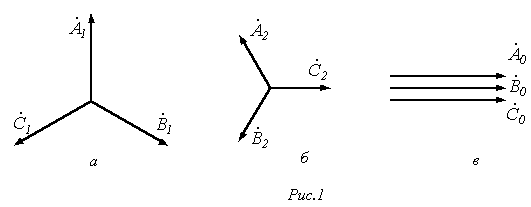
Симметричную систему прямой последовательности образуют (см. рис. 1,а) три одинаковых по модулю вектора 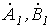 и
и 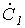 со сдвигом друг по отношению к другу на
со сдвигом друг по отношению к другу на 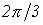 рад., причем
рад., причем 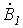 отстает от
отстает от 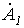 , а
, а 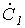 - от
- от 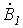 .
.
Введя оператор поворота 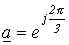 , для симметричной системы прямой последовательности можно записать
, для симметричной системы прямой последовательности можно записать
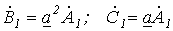 .
.
Симметричная система обратной последовательности образована равными по модулю векторами 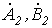 и
и 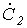 с относительным сдвигом по фазе на
с относительным сдвигом по фазе на 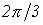 рад., причем теперь
рад., причем теперь 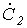 отстает от
отстает от 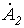 , а
, а 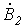 - от
- от 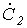 (см. рис. 1,б). Для этой системы имеем
(см. рис. 1,б). Для этой системы имеем
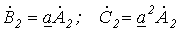 .
.
Система нулевой последовательности состоит из трех векторов, одинаковых по модулю и фазе (см. рис. 1,в):
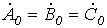 .
.
Любая несимметричная система однозначно раскладывается на симметричные составляющие. Действительно,
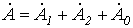 ; (1)
; (1)
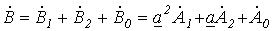 ; (2)
; (2)
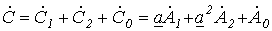 . (3)
. (3)
Таким образом, получена система из трех уравнений относительно трех неизвестных 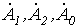 , которые, следовательно, определяются однозначно. Для нахождения
, которые, следовательно, определяются однозначно. Для нахождения 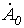 сложим уравнения (1)…(3). Тогда, учитывая, что
сложим уравнения (1)…(3). Тогда, учитывая, что 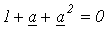 , получим
, получим
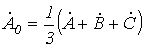 . (4)
. (4)
Для нахождения 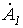 умножим (2) на
умножим (2) на 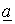 , а (3) – на
, а (3) – на 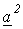 , после чего полученные выражения сложим с (1). В результате приходим к соотношению
, после чего полученные выражения сложим с (1). В результате приходим к соотношению
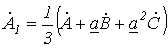 . (5)
. (5)
Для определения 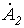 с соотношением (1) складываем уравнения (2) и (3), предварительно умноженные соответственно на
с соотношением (1) складываем уравнения (2) и (3), предварительно умноженные соответственно на 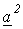 и
и 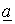 . В результате имеем:
. В результате имеем:
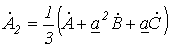 . (6)
. (6)
Формулы (1)…(6) справедливы для любой системы векторов 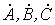 , в том числе и для симметричной. В последнем случае
, в том числе и для симметричной. В последнем случае 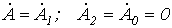 .
.
 2015-04-23
2015-04-23 464
464








