2015-04-23
849
Аналитическое выравнивание ряда динамики
Цель задания: освоить методику выравнивания ряда динамики с использованием аналитических функций в MicrosoftExcel
Общую тенденцию изменения объема товарооборота выразим уравнением параболы 2-го порядка.
На графике (рис…) заметна тенденция роста объема товарооборота с определённым ускорением начиная с 2010 года. Снижение уровня в 2008 году можно считать случайным.
Уравнение тренда в общем виде (основная тенденция) имеет вид:
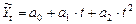
Для определения параметров уравнения способом наименьших квадратов необходимо решить следующую систему уравнений:
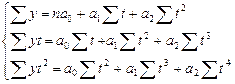
Для решения системы уравнений необходимо на основе данных ряда динамики определить числовые параметры (таблица 1)
Таблица 1 – Расчетные показатели для определения параметров уравнения тренда и теоретических уровней.
| Годы | Уровни Yi | Обозначение времени, ti | Расчетные величины | ||||
| 
| 
| 
| 
| |||
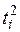
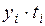
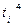
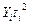
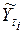
| -2,5 | 6,25 | -1480,0 | 39,0625 | 3700,00 | 611,1 | ||
| -1,5 | 2,25 | -958,5 | 5,0625 | 1437,75 | 599,1 | ||
| -0,5 | 0,25 | -307,5 | 0,0625 | 153,75 | 623,3 | ||
| 0,5 | 0,25 | 332,5 | 0,0625 | 166,25 | 683,7 | ||
| 1,5 | 2,25 | 1170,0 | 5,0625 | 1755,00 | 780,3 | ||
| 2,5 | 6,25 | 2300,0 | 39,0625 | 5750,00 | 913,1 | ||
| Сумма | 17,5 | 1056,5 | 88,375 | 12962,75 | 4210,7 |
При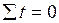 
(способ обозначения «t» при котором начало отсчета «0» переносится в середину периода представлен в таблице 1) решение системы уравнений упрощается:
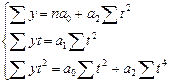
Подставим данные из таблицы 1 в систему уравнений:
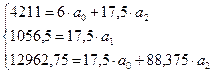
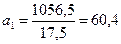
Далее решается система 2-х уравнений:
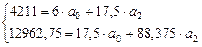
Члены каждого из уравнений делим на коэффициент при a0
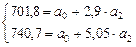
Из второго уравнения вычитаем первое:
38,9 = 2,15 a2
a2 = 38,9: 2,15 = 18,1
Подставляя найденное значениеa2в одно из уравнений, находим:
4211 = 6 a0 + 17,5 ´ 18,1
a0 = 649,04» 649
Уравнение тренда принимает вид:
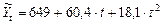
Подставляя в уравнение значение “t” находим теоретические значения уровней (графа 8 таблицы 1)
Прогнозное значение размера товарооборота найдём, подставляя в уравнение тренда обозначение”t”.
В 2012 году “t” будет равно 3,5, тогда прогнозируемый уровень составит: 649 + 60,4*3,5 + 18,1*12,25 = 1082,1 (млн. руб.).
Ожидаемое значение объёма розничного товарооборота в 2012 году составило 1083,1 млн. рублей.
Используем для выравнивания ряда динамики линейную функцию:
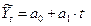
Для определения параметров уравнения способом наименьших квадратов необходимо решить следующую систему уравнений:
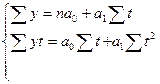
При данном способе обозначения «t» решение системы уравнений упрощается, так как исключаются слагаемые, равные «0».
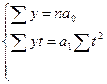, откуда 
; 
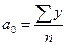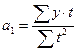
Подставляя в формулы данные таблицы 1 получаем:
;
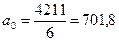Значение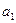 
уже найдено при расчёте уравнения параболы
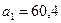
Уравнение тренда принимает вид:
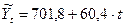
Уравнение характеризует тенденцию роста товарооборота в среднем ежегодно на 60,4 млн. руб., при среднегодовом объёме товарооборота 701,8 млн. руб.
Значения параметра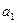 
(скорость роста) в уравнении прямой и параболы второго порядка совпадают. Однако, линейная функция характеризует равномерный рост, а парабола - рост с определённым ускорением (
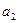= 18,1).
Определим теоретические уровни ряда динамики на основе полученного линейного тренда:
Таблица 2- Фактические и теоретические значения уровней ряда динамики
| Год | Фактические уровни Yi | Теоретические уровни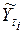
|
| 550,8 | ||
| 611,2 | ||
| 671,6 | ||
| 732,0 | ||
| 792,4 | ||
| 852,8 | ||
| Сумма | 4210,8 |
Сумма фактических уровней равна сумме теоретических уровней, что подтверждает правильность вычислений, так как способ наименьших квадратов обеспечивает автоматическое равенство указанных сумм для прямой и парабол любого порядка,
Прогнозное значение размера товарооборота найдём, подставляя в уравнение тренда обозначение”t”.
В 2012 году “t” будет равно 3,5, тогда прогнозируемый уровень составит: 701,8 + 60,4*3,5 =913,2 (млн. руб.).
Ожидаемое значение объёма розничного товарооборота в 2012 году составило 913,2 млн. рублей.
